题目内容
【题目】如图，已知直线与抛物线y2=2px（p＞0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于点D（不为原点）．
（Ⅰ）求点D的轨迹方程；
（Ⅱ）若点D坐标为（2，1），求p的值．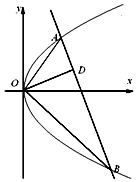
【答案】解：（Ⅰ）设点A的坐标（x1 ， y1），点B的坐标（x2 ， y2），点D的坐标为（x0 ， y0）（x0≠0）， 由OA⊥OB得x1x2+y1y2=0．
由已知，得直线AB的方程为 
．
又有 
，
由x1x2+y1y2=0得 
．
把 代入y2=2px并消去x得 
，
得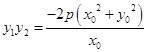 
代入
得 
故所求点D的轨迹方程为x2+y2﹣2px=0（x≠0）．
（Ⅱ）把x=2，y=1代入方程x2+y2﹣2px=0中，得 
【解析】（Ⅰ）设点A的坐标（x1 ， y1），点B的坐标（x2 ， y2），点D的坐标为（x0 ， y0）（x0≠0），由OA⊥OB，得x1x2+y1y2=0，由此入手能求出点D的方程．（Ⅱ）点D（2，1）代入方程x2+y2﹣2px=0，能求出结果．
练习册系列答案
相关题目
