题目内容
设椭圆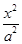 +
+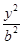 =1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为 ( )
=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为 ( )
A. ab ab | B.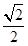 ab ab | C.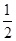 ab ab | D.2ab |
B
解析试题分析:设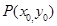
 ,则有
,则有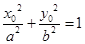 ,即
,即 ;又因为
;又因为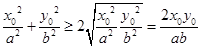 ,即
,即 ,所以
,所以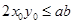 。
。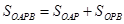 =
= ,所以
,所以 ,即
,即 ,故B正确。
,故B正确。
考点:椭圆基本性质,基本不等式,分割法求面积

练习册系列答案
相关题目
若 ,且
,且 ,则下列不等式中,恒成立的是
,则下列不等式中,恒成立的是
A. | B. |
C. | D. |
若实数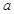 ,
, 满足
满足 ,则
,则 的最小值是
的最小值是
| A.18 | B.6 | C.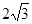 | D. |
下列说法中,正确的是( )
A.当x>0且x≠1时,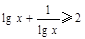 | B.当x>0时,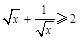 |
C.当x≥2时,x+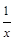 的最小值为2 的最小值为2 | D.当0<x≤2时,x-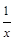 无最大值 无最大值 |
已知直线 (
( )经过圆
)经过圆 的圆心,则
的圆心,则 的最小值是( )
的最小值是( )
| A.9 | B.8 | C.4 | D.2 |
设a,b满足2a+3b=6,a>0,b>0,则 +
+ 的最小值为( )
的最小值为( )
A. | B. | C. | D.4 |
已知实数 ,
, ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
若 ( )
( )
A. | B. | C. | D. |
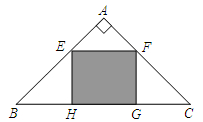
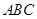 的空地,要在这块空地上开辟一个内接矩形
的空地,要在这块空地上开辟一个内接矩形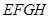 的绿地,已知
的绿地,已知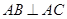 ,
,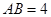 ,绿地面积最大值为( )
,绿地面积最大值为( )