题目内容
10. 如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.
如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.(1)若∠D=∠ABD,BC=2$\sqrt{3}$,AC=4,求△ABC外接圆的面积;
(2)求证:AC•EF=AB•EC.
分析 (1)利用切割线定理,求出DA,证明AC为△ABC外接圆的直径,即可求△ABC外接圆的面积;
(2)证明△EFC∽△ABC,即可证明AC•EF=AB•EC.
解答 (1)解:∵BD是△ABC外接圆的切线,
∴∠C=∠ABD,
∵∠D=∠ABD,
∴∠D=∠C,
∴BD=BC=2$\sqrt{3}$,
由切割线定理可得BD2=DA•DC,即12=DA•(DA+4),
∴DA=2,
∵∠D=∠ABD,
∴AB=AD=2,
∴△ABC中,AB2+BC2=AC2,∴AC为△ABC外接圆的直径,
∴△ABC外接圆的面积为4π•22=16π;
(2)证明:连接CF,则∠ECF=∠BAF=∠ACB,
∵∠EFC=∠ABC,
∴△EFC∽△ABC,
∴$\frac{EF}{AB}=\frac{EC}{AC}$,
∴AC•EF=AB•EC.
点评 本题考查切割线定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
10.函数f(x)=lg(1-x)+lg(3x+1)的定义域是( )
| A. | [-$\frac{1}{3}$,1] | B. | (-$\frac{1}{3}$,$\frac{1}{3}$) | C. | (-$\frac{1}{3}$,1) | D. | (-∞,-$\frac{1}{3}$) |
2.已知PA垂直于△ABC所在的平面,AB=AC=5,BC=6,PA=3,则点A到平面PBC的距离为( )
| A. | 4 | B. | $\sqrt{15}$ | C. | $3\sqrt{5}$ | D. | $\frac{12}{5}$ |
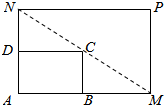 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米. 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.