题目内容
19.设函数f(x)是定义在R上的函数,对定义域内的任意x,y都有f(x+y)=f(x)+f(y),且f(-1)=2.当x>0时,f(x)<0.(1)判断f(x)的奇偶性;
(2)求f(x)在x∈[-3,5]时的最大值和最小值;
(3)若f(m)+$\frac{1}{2}$f(9)>$\frac{1}{2}$f(m2)+f(3),求实数m的取值范围.
分析 (1)利用赋值法求f(0)的值,即可判断f(x)的奇偶性;
(2)根据函数单调性的定义即可判断函数单调性,根据函数的单调性和最值之间的关系即可得到结论;
(3)利用f(m)+$\frac{1}{2}$f(9)>$\frac{1}{2}$f(m2)+f(3),可得f(2m+9)>f(m2+6),根据f(x)在R上是减函数,即可得出结论.
解答 解:(1)令x=y=0,可得f(0)=0,
令y=-x,可得f(0)=f(x)+f(-x)=0,∴f(x)是奇函数;
(2)设x1>x2,f(x)+f(y)=f(x+y),令x=x2,x+y=x1,
则y=x1-x2>0,
∴f(x2)+f(x1-x2)=f(x1),
∴f(x1)-f(x2)=f(x1-x2)<0,
∴f(x)在R上是减函数;
∵f(-3)=3f(-1)=6,f(5)=5f(1)=-10,
∴最大值为f(-3)=6,最小值为f(5)=-10;
(3)∵f(m)+$\frac{1}{2}$f(9)>$\frac{1}{2}$f(m2)+f(3),
∴2f(m)+f(9)>f(m2)+2f(3),
∴f(2m+9)>f(m2+6),
∵f(x)在R上是减函数,
∴2m+9<m2+6,
∴m<-1或m>3.
点评 本题主要考查抽象函数的应用,根据定义法和赋值法是解决抽象函数问题的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.函数f(x)=lg(1-x)+lg(3x+1)的定义域是( )
| A. | [-$\frac{1}{3}$,1] | B. | (-$\frac{1}{3}$,$\frac{1}{3}$) | C. | (-$\frac{1}{3}$,1) | D. | (-∞,-$\frac{1}{3}$) |
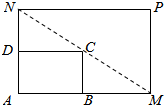 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.