题目内容
【题目】如图，在△ABC中，CD是∠ACB的角平分线，△ADC的外接圆交BC于点E，AB=2AC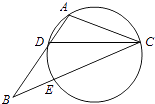
（1）求证：BE=2AD；
（2）当AC=3，EC=6时，求AD的长．
【答案】
（1）
证明：连接DE，
∵ACED是圆内接四边形，
∴∠BDE=∠BCA，
又∠DBE=∠CBA，∴△DBE∽△CBA，即有 
，
又∵AB=2AC，∴BE=2DE，
∵CD是∠ACB的平分线，∴AD=DE，
∴BE=2AD；
（2）
解：由条件知AB=2AC=6，设AD=t，
则BE=2t，BC=2t+6，
根据割线定理得BDBA=BEBC，
即（6﹣t）×6=2t（2t+6），即2t2+9t﹣18=0，
解得 
或﹣6（舍去），则 
．
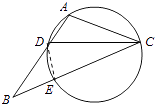
【解析】（1）连接DE，证明△DBE∽△CBA，利用AB=2AC，结合角平分线性质，即可证明BE=2AD；（2）根据割线定理得BDBA=BEBC，从而可求AD的长．
练习册系列答案
相关题目
