题目内容
【题目】定义在R上的奇函数f(x)满足f(x﹣2)=f(x+2),且当x∈[﹣2,0]时,f(x)=3x﹣1,则f(9)=( )
A.﹣2
B.2
C.![]()
D.![]()
【答案】D
【解析】解:根据题意,函数f(x)满足f(x﹣2)=f(x+2),即f(x)=f(x+4),
则函数f(x)的周期为4,
f(9)=f(1),
又由函数f(x)为奇函数,则f(1)=﹣f(﹣1),
又由当x∈[﹣2,0]时,f(x)=3x﹣1,
则f(﹣1)=3﹣1﹣1= ![]() ﹣1=﹣
﹣1=﹣ ![]() ;
;
则有f(9)=f(1)=﹣f(﹣1)= ![]() ;
;
故选:D.
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图: 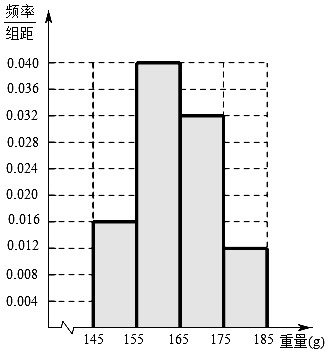
(Ⅰ)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(Ⅱ)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [165,185] | [155,165) | [145,155) |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中,  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
