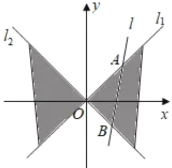
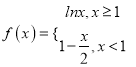题目内容
【题目】已知平面向
，满足
，且
，
与
夹角余弦值的最小值等于_________.
【答案】
【解析】
根据平面向量数量积的运算律化简
,结合题中所给模长用
表示出
,即可用表示出
与
夹角
的余弦值;利用换元法令
,由平面向量数量积定义及三角函数的值域,求得
的范围.代入
中求得m的取值范围.再根据平面向量数量积定义,用m表示出
与夹角余弦值,即可由m的取值范围结合表达式的性质得解.
平面向
,满足
,则
因为
展开化简可得
,
因为
,代入化简可得
设与的夹角为
则由上式可得
而
代入上式化简可得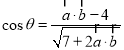
令,设
与
的夹角为
,则由平面向量数量积定义可得
,而
所以
由余弦函数的值域可得,即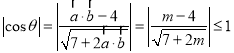
将不等式化简可得
,解不等式可得
综上可得
,即
而由平面向量数量积的运算可知,设与夹角为
,
则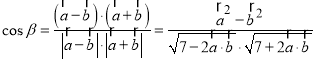
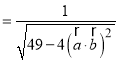
当分母越大时,
的值越小;当的值越小时,分母的值越大
所以当
时, 的值最小
代入可得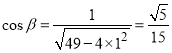
所以与夹角余弦值的最小值等于
故答案为:
【题目】2019年某地初中毕业升学体育考试规定：考生必须参加长跑、掷实心球、1分钟跳绳三项测试，三项测试各项20分，满分60分．某学校在初三上学期开始时，为掌握全年级学生1分钟跳绳情况，按照男女比例利用分层抽样抽取了100名学生进行测试，其中女生54人，得到下面的频率分布直方图，计分规则如表1：
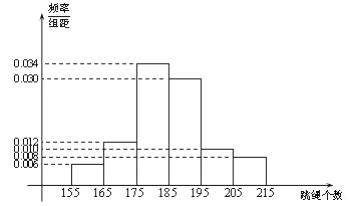
表1
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）规定：学生1分钟跳绳得分20分为优秀，在抽取的100名学生中，男生跳绳个数大于等于185个的有28人，根据已知条件完成表2，并根据这100名学生测试成绩，能否有99%的把握认为学生1分钟跳绳成绩优秀与性别有关？
表2
跳绳个数 |
|
| 合计 |
男生 | 28 | ||
女生 | 54 | ||
合计 | 100 |
附：参考公式：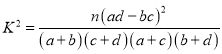
临界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）根据往年经验，该校初三年级学生经过一年的训练，正式测试时每人每分钟跳绳个数都有明显进步．假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个，全年级恰有2000名学生，所有学生的跳绳个数
服从正态分布
（用样本数据的平均值和方差估计总体的期望和方差，各组数据用中点值代替）．
①估计正式测试时，1分钟跳182个以上的人数（结果四舍五入到整数）；
②若在全年级所有学生中任意选取3人，正式测试时1分钟跳195个以上的人数为
，求的分布列及期望．
附：若随机变量服从正态分布，则
，
，
．
．
【题目】为了解儿子身高与其父亲身高的关系，随机调查了5对父子的身高，统计数据如下表所示．
编 号 | A | B | C | D | E |
父亲身高 | 174 | 176 | 176 | 176 | 178 |
儿子身高 | 175 | 175 | 176 | 177 | 177 |
（1）从这五对父子任意选取两对，用编号表示出所有可能取得的结果，并求随机事件
“两对父子中儿子的身高都不低于父亲的身高”发生的概率；
（2）由表中数据，利用“最小二乘法”求
关于
的回归直线的方程．
参考公式：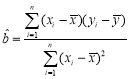
，
；回归直线：
．
