题目内容
已知函数f(x)= sin
sin .
.
(1)求它的振幅、周期、初相;
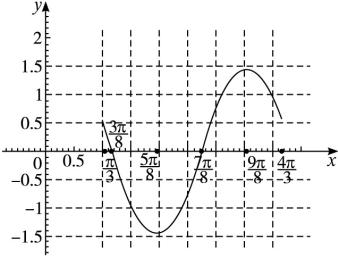
(2)在所给坐标系中用五点法作出它在区间 上的图象.
上的图象.
(3)说明y=sin x的图像可由y= sin
sin 的图像经过怎样的变换而得到.
的图像经过怎样的变换而得到.
 sin
sin .
.(1)求它的振幅、周期、初相;
(2)在所给坐标系中用五点法作出它在区间
 上的图象.
上的图象.(3)说明y=sin x的图像可由y=
 sin
sin 的图像经过怎样的变换而得到.
的图像经过怎样的变换而得到.
(1)y= sin
sin 的振幅A=
的振幅A= ,周期T=
,周期T=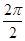 =π,初相φ=
=π,初相φ=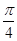 .
.
(2)
(3)y=sin x的图像可由y= sin
sin 的图像,先将所有点的纵坐标缩短为原来的
的图像,先将所有点的纵坐标缩短为原来的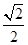 倍,同时周期扩大为原来的2倍,同时向左平移
倍,同时周期扩大为原来的2倍,同时向左平移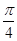 个单位得到。
个单位得到。
 sin
sin 的振幅A=
的振幅A= ,周期T=
,周期T=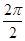 =π,初相φ=
=π,初相φ=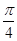 .
.(2)

(3)y=sin x的图像可由y=
 sin
sin 的图像,先将所有点的纵坐标缩短为原来的
的图像,先将所有点的纵坐标缩短为原来的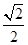 倍,同时周期扩大为原来的2倍,同时向左平移
倍,同时周期扩大为原来的2倍,同时向左平移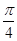 个单位得到。
个单位得到。试题分析:(1)y=
 sin
sin 的振幅A=
的振幅A= ,周期T=
,周期T=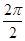 =π,初相φ=
=π,初相φ=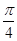 .
.列表:
2x+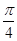 | π | 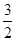 π π | 2π | 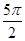 |
| x | 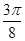 | 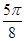 | 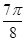 | 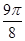 |
f(x)= sin sin | 0 | - | 0 |  |
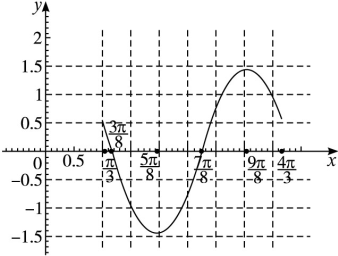
(3)略.
点评:解决的关键是根据三角函数解析式来五点法作图,同时能结合三角函数的图像的变换来求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
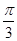 )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移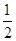 x
x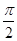 )
)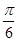 )
)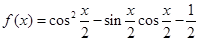 .
.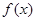 的最小正周期和值域;
的最小正周期和值域;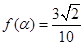 ,求
,求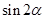 的值.
的值.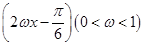 的图象过点
的图象过点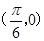 ,在[0,
,在[0, 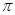 ]上的单调递增区间为________
]上的单调递增区间为________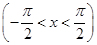 的大致图象是( )
的大致图象是( )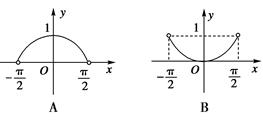
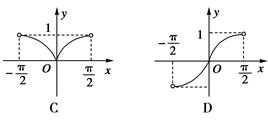
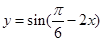 的单调减区间是
的单调减区间是 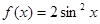 的最小正周期是_____________
的最小正周期是_____________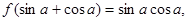 若
若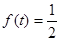 ,则
,则 的值为 ( )
的值为 ( )



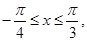 则函数
则函数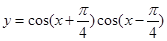 的值域为________.
的值域为________.