Question

【题目】某中学为了普及奥运会知识和提高学生参加体育运动的积极性，举行了一次奥运知识竞赛．随机抽取了30名学生的成绩，绘成如图所示的茎叶图，若规定成绩在75分以上（包括75分）的学生定义为甲组，成绩在75分以下（不包括75分）定义为乙组．
（Ⅰ）在这30名学生中，甲组学生中有男生7人，乙组学生中有女生12人，试问有没有90%的把握认为成绩分在甲组或乙组与性别有关；
（Ⅱ）记甲组学生的成绩分别为x1 ， x2 ， …，x12 ， 执行如图所示的程序框图，求输出的S的值；
（Ⅲ）竞赛中，学生小张、小李同时回答两道题，小张答对每道题的概率均为 ，小李答对每道题的概率均为 ，两人回答每道题正确与否相互独立．记小张答对题的道数为a，小李答对题的道数为b，X=|a﹣b|，写出X的概率分布列，并求出X的数学期望．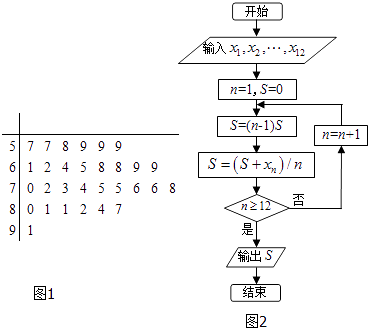

附：K2= ；其中n=a+b+c+d
独立性检验临界表：

P（K2＞k0）	0.100	0.050	0.010
k0	2.706	3.841	6.635

Answer 1

【答案】解：（Ⅰ）作出2×2列联表：

	甲组	乙组	合计
男生	7	6	13
女生	5	12	17
合计	12	18	30

由列联表数据代入公式，计算得K2= = ≈1.83，
因为1.83＜2.706，故没有90%的把握认为成绩分在甲组或乙组与性别有关；
（Ⅱ）根据程序运行的过程，得出该程序运行后输出的是求甲组数据的平均数，
所以输出S= ×（75+75+76+76+78+80+81+81+82+84+87+91）=80.5；
（Ⅲ）由已知得X的可能取值为0，1，2，
P（X=0）=（1﹣ ）（1﹣ ）（1﹣ ）+ （1﹣ ） = ，
P（X=1）= （1﹣ ）（1﹣ ）+（1﹣ ）（1﹣ ） + = ，
P（X=2）= （1﹣ ）= ，
∴X的分布列为：

X	0	1	2
P

X的数学期望值为EX=0× +1× +2× =
【解析】（Ⅰ）作2×2列联表，计算K2 ， 对照数表即可得出结论；（Ⅱ）根据程序运行的过程，得出该程序运行后输出的是求平均数，求出即可；（Ⅲ）由已知得X的可能取值，计算对应的概率值，写出X的分布列，计算数学期望值．
【考点精析】根据题目的已知条件，利用离散型随机变量及其分布列的相关知识可以得到问题的答案，需要掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．