题目内容
14.设变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$则z=|x-3y|的取值范围为( )| A. | [2,8] | B. | [0,8] | C. | [4,8] | D. | [0,4] |
分析 由约束条件作差可行域,令t=x-3y,化为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入t=x-3y求出t的范围,则答案可求.
解答 解:由约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$作差可行域如图,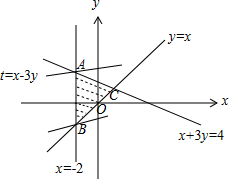
令t=x-3y,化为直线方程的斜截式得y=$\frac{1}{3}x-\frac{t}{3}$,
联立$\left\{\begin{array}{l}{x=-2}\\{x+3y=4}\end{array}\right.$,解得:A(-2,2),
联立$\left\{\begin{array}{l}{x=-2}\\{y=x}\end{array}\right.$,解得:B(-2,-2),
由图可知,当直线y=$\frac{1}{3}x-\frac{t}{3}$过B时,直线在y轴上的截距最小,t有最大值为-2-3×(-2)=4;
当直线y=$\frac{1}{3}x-\frac{t}{3}$过A时,直线在y轴上的截距最大,t有最小值为-2-3×2=-8.
∴z=|x-3y|的取值范围是[0,8].
故选:B.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.等差数列{an}中,a${\;}_{m}=\frac{1}{k}$,ak=$\frac{1}{m}$(m≠k),则该数列前mk项之和为( )
| A. | $\frac{mk}{2}-1$ | B. | $\frac{mk}{2}$ | C. | $\frac{mk+1}{2}$ | D. | $\frac{mk}{2}+1$ |
3.已知函数f(x)=loga(2x+b-1)的部分图象如图所示,则a,b所满足的关系是( )


| A. | 0<b-1<a<1 | B. | 0<a-1<b<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b-1<1 |
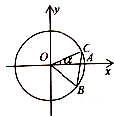 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.