题目内容
9.已知等比数列{an}满足an+1+an=9•2n-1,n∈N*,设数列{an}的前n项和为Sn.若不等式Sn>kan-2对一切n∈N*恒成立,则实数k的取值范围是(-∞,$\frac{5}{3}$).分析 利用等比数列{an}满足an+1+an=9•2n-1确定数列的公比与首项、求出an、Sn,再利用不等式Sn>kan-2,分离参数、求最值,进而即可求实数k的取值范围.
解答 解:设等比数列{an}的公比为q,
∵an+1+an=9•2n-1,n∈N*,
∴当n=1时,有:a2+a1=9,
当n=2时,有:a3+a2=18,
∴q=$\frac{{a}_{3}+{a}_{2}}{{a}_{2}+{a}_{1}}$=$\frac{18}{9}$=2,
又∵a2+a1=2a1+a1=9,
∴a1=3,
∴an=3•2n-1,Sn=$\frac{3(1-{2}^{n})}{1-2}$=3•2n-3,
∵不等式Sn>kan-2对一切n∈N*恒成立,
即3•2n-3>3k•2n-1-2,
∴k<2-$\frac{1}{3•{2}^{n-1}}$≤2-$\frac{1}{3•{2}^{1-1}}$=$\frac{5}{3}$,
∴k∈(-∞,$\frac{5}{3}$),
故答案为:(-∞,$\frac{5}{3}$).
点评 本题考查数列递推式,考查等比数列的通项与求和,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.下图几何体是由选项中的哪个平面图旋转而得到的( )
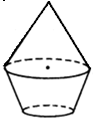

| A. | 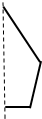 | B. | 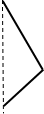 | C. | 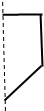 | D. |  |
1.方程x2+y2+2ax-2ay=0(a≠0)表示的圆( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x-y=0对称 | D. | 关于直线x+y=0对称 |
19.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,
得到下面的散点图及一些统计量的值.
其中wi=$\sqrt{{x}_{i}}$,$\overline{w}$=$\frac{1}{8}$$\sum_{i=1}^{8}{w}_{i}$
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.

得到下面的散点图及一些统计量的值.
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})({y}_{i}-\overline{y)}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.

 如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.