题目内容
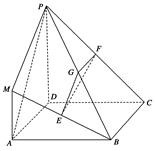
在如图所示的几何体中,四边形 是正方形,
是正方形, ⊥平面
⊥平面 ,
,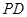 ∥
∥ ,
,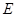 、
、 、
、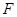 分别为
分别为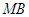 、
、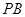 、
、 的中点,且
的中点,且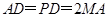 .
.
(1)求证:平面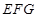 ⊥平面
⊥平面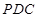 ;
;
(2)求三棱锥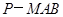 与四棱锥
与四棱锥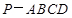 的体积之比.
的体积之比.
(1)主要证明
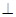 平面
平面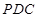 (2)
(2)
解析试题分析:解:(1)证明:∵
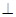 平面
平面 ,
,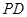 ∥
∥ ,
,
∴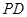
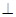 平面
平面 ,
,
又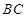
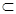 平面
平面 ,∴
,∴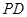
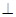
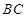 ,
,
∵ 为正方形,∴
为正方形,∴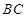
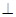 DC.
DC.
∵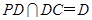 ,∴
,∴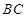
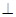 平面
平面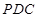 .
.
在 中,因为
中,因为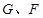 分别为
分别为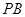 、
、 的中点,
的中点,
∴ ∥
∥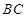 ,∴
,∴
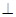 平面
平面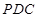 .
.
又
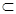 平面
平面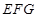 ,∴平面
,∴平面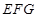
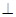 平面
平面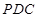 .
.
(2)不妨设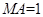 ,∵
,∵ 为正方形,∴
为正方形,∴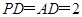 ,
,
又∵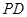
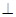 平面
平面 ,
,
所以 =
=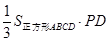 =
= .
.
由于
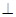 平面
平面 ,且
,且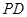 ∥
∥ ,
,
所以 即为点
即为点 到平面
到平面 的距离,
的距离,
三棱锥 =
= ×
× ×2=
×2= .
.
所以 .
.
考点:平面与平面垂直的判定;棱柱、棱锥、棱台的体积.
点评:本题考查空间中的线面关系,考查线面垂直、面面垂直的判定及几何体体积的计算,考查试图能力和逻辑思维能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
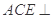 平面
平面 ,四边形
,四边形 .
.
 平面
平面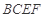 ;
;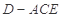 的体积.
的体积. 的边长为3,点
的边长为3,点 、
、 分别是边
分别是边 、
、 上的点,且满足
上的点,且满足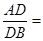
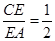 (如图1).将△
(如图1).将△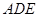 沿
沿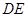 折起到△
折起到△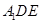 的位置,使二面角
的位置,使二面角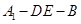 成直二面角,连结
成直二面角,连结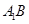 、
、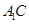 (如图2).
(如图2).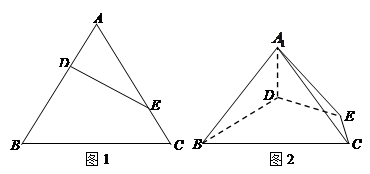
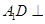 平面
平面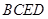 ;
; 上是否存在点
上是否存在点 ,使直线
,使直线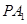 与平面
与平面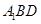 所成的角为
所成的角为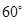 ?若存在,求出
?若存在,求出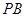 的长,若不存在,请说明理由.
的长,若不存在,请说明理由. 的侧棱与底面
的侧棱与底面 垂直,底面
垂直,底面 ,侧棱
,侧棱 ,
, 分别是
分别是 与
与 的中点,点
的中点,点 在平面
在平面 上的射影是
上的射影是 的垂心
的垂心

 ;
; 中(图1),
中(图1),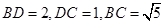 ,
,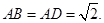
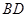 中点为
中点为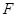 ,将图1沿直线
,将图1沿直线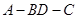 为
为 (图2)
(图2)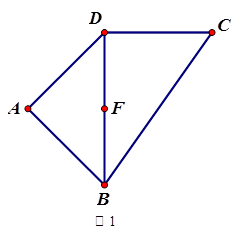
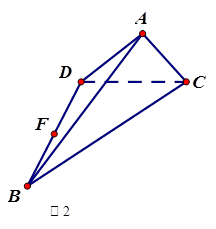
 作直线
作直线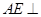 平面
平面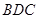 ,且
,且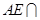 平面
平面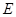 ,求
,求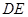 的长度。
的长度。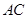 与平面
与平面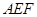 所成角的正弦值。
所成角的正弦值。 ,
, ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使 且
且 ,得一简单组合体
,得一简单组合体 如图2示,已知
如图2示,已知 分别为
分别为 的中点.
的中点.

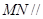 平面
平面 ;
; 
 ;
; 多长时,平面
多长时,平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ?
? 中,D,E分别是AB,BB1的中点,
中,D,E分别是AB,BB1的中点, =AC=CB=
=AC=CB= AB.
AB.
 //平面
//平面 ;
; -E的正弦值.
-E的正弦值.



 是菱形,
是菱形, 是矩形,平面
是矩形,平面 ,
, ,
, ,
, 是
是 的中点.
的中点.
 //平面
//平面 ;
; 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长
的长 ;若不存在,请说明理由.
;若不存在,请说明理由.