题目内容
【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等制划分标准为:85分及以上,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;60分以下,记为
等;60分以下,记为![]() 等.同时认定
等.同时认定![]() 为合格,
为合格, ![]() 为不合格.已知甲,乙两所学校学生的原始成绩均分布在
为不合格.已知甲,乙两所学校学生的原始成绩均分布在![]() 内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照
内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照![]() 的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为
的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为![]() 的所有数据茎叶图如图2所示.
的所有数据茎叶图如图2所示.
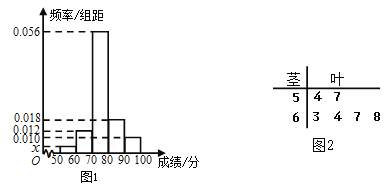
(Ⅰ)求图1中![]() 的值,并根据样本数据比较甲乙两校的合格率;
的值,并根据样本数据比较甲乙两校的合格率;
(Ⅱ)在选取的样本中,从甲,乙两校![]() 等级的学生中随机抽取3名学生进行调研,用
等级的学生中随机抽取3名学生进行调研,用![]() 表示所抽取的3名学生中甲校的学生人数,求随机变量
表示所抽取的3名学生中甲校的学生人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;甲、乙两校的合格率均为96%;(2)详见解析.
;甲、乙两校的合格率均为96%;(2)详见解析.
【解析】试题分析:(1)频率分布直方图中,小矩形的和为频率和,和为1,这样可得到![]() 的值;合格率为大于等于60分的频率和;(2)
的值;合格率为大于等于60分的频率和;(2)![]() 为
为![]() 级,甲校C级的频率为
级,甲校C级的频率为![]() ,人数为
,人数为![]() ,而乙校C级的人数为4人,随机抽取3人中,甲校学生人数
,而乙校C级的人数为4人,随机抽取3人中,甲校学生人数![]() 的可能取值为0,1,2,3,所对应的概率
的可能取值为0,1,2,3,所对应的概率![]() ,列分布列并求数学期望.
,列分布列并求数学期望.
试题解析:(1)由题意,可知![]() ,
,
∴![]() ................2分
................2分
∴甲学校的合格率为![]() ........................3分
........................3分
而乙学校的合格率为![]() .................4分
.................4分
∴甲、乙两校的合格率均为96%................5分
(2)样本中甲校![]() 等级的学生人数为
等级的学生人数为![]() ....................6分
....................6分
而乙校![]() 等级的学生人数为4.
等级的学生人数为4.
∴随机抽取3人中,甲校学生人数![]() 的可能取值为0,1,2,3...........7分
的可能取值为0,1,2,3...........7分
∴![]() ,
,
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
...................................11分
数学期望![]() .................12分
.................12分