题目内容
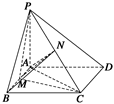
如图,已知三棱锥P-ABC中,PA、PB、PC与底面ABC成相等的角,∠CAB=90°,AC=AB,D为BC的中点,E点在PB上,PC∥截面EAD.
(1)求证:平面PBC⊥底面ABC.
(2)若AB=PB,求AE与底面ABC所成角的正弦值.

(1)求证:平面PBC⊥底面ABC.
(2)若AB=PB,求AE与底面ABC所成角的正弦值.
(1)证明:∵PA、PB、PC与底面ABC成等角,
∴顶点P在底面上的射影为底面Rt△CAB的外心.
而Rt△CAB的外心在斜边BC的中点D处,
即PD⊥平面ABC,
而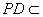 平面PBC,
平面PBC,
∴平面PBC⊥底面ABC.
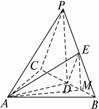
(2)解:∵PC∥截面EAD, 平面PBC,
平面PBC,
且平面PBC∩平面EAD=DE,
∴PC∥DE,而D为BC中点,
∴E为PB的中点.
过E作EM∥PD,
则EM与BC的交点M为BD的中点,连结AM,
∵PD⊥底面ABC,∴EM⊥底面ABC.
∴∠EAM为AE与底面ABC所成的角.
设AB=AC=PB=a,则 ,
,
而PB=PC=a,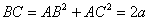 ,
,
∴PB2+PC2=BC2.
∴△CPB为等腰直角三角形.
∴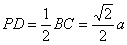 ,
, .
.
在Rt△AEM中, .
.
∴AE与底面ABC所成角的正弦值为 .
.
∴顶点P在底面上的射影为底面Rt△CAB的外心.
而Rt△CAB的外心在斜边BC的中点D处,
即PD⊥平面ABC,
而
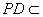 平面PBC,
平面PBC,∴平面PBC⊥底面ABC.
(2)解:∵PC∥截面EAD,
 平面PBC,
平面PBC,且平面PBC∩平面EAD=DE,
∴PC∥DE,而D为BC中点,
∴E为PB的中点.
过E作EM∥PD,
则EM与BC的交点M为BD的中点,连结AM,
∵PD⊥底面ABC,∴EM⊥底面ABC.
∴∠EAM为AE与底面ABC所成的角.
设AB=AC=PB=a,则
 ,
,而PB=PC=a,
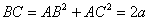 ,
,∴PB2+PC2=BC2.
∴△CPB为等腰直角三角形.
∴
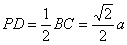 ,
, .
.在Rt△AEM中,
 .
.∴AE与底面ABC所成角的正弦值为
 .
.空间直线和平面

练习册系列答案
相关题目
 中,E、F分别是
中,E、F分别是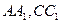 的中点,
的中点,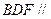 平面
平面
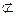 α ,m
α ,m α ,l∥m
α ,l∥m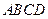 ,
,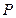 ,
,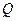 分别是△
分别是△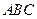 和△
和△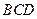 的重心.
的重心. 平面
平面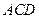 .
.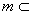 平面β,给出下列命题:
平面β,给出下列命题: 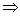 l∥M;
l∥M;