题目内容
正三棱柱的底面边长为2,高为2,则它的外接球表面积为
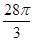

试题分析:由正三棱柱的底面边长为2,易得底面所在平面截其外接圆O的半径
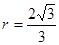 ,又由正三棱柱的高为2,则球心到圆O的球心距
,又由正三棱柱的高为2,则球心到圆O的球心距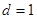 ,根据球心距,截面圆半径,球半径构成直角三角形, 满足勾股定理,我们易得球半径R满足:
,根据球心距,截面圆半径,球半径构成直角三角形, 满足勾股定理,我们易得球半径R满足: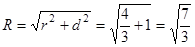
故外接球的表面积
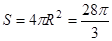

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
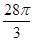

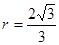 ,又由正三棱柱的高为2,则球心到圆O的球心距
,又由正三棱柱的高为2,则球心到圆O的球心距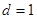 ,根据球心距,截面圆半径,球半径构成直角三角形, 满足勾股定理,我们易得球半径R满足:
,根据球心距,截面圆半径,球半径构成直角三角形, 满足勾股定理,我们易得球半径R满足: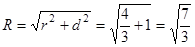
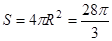

 阅读快车系列答案
阅读快车系列答案