题目内容
已知矩阵A的逆矩阵A-1=
,求矩阵A的特征值.
|
考点:逆变换与逆矩阵
专题:选作题,矩阵和变换
分析:先求出矩阵A,再求矩阵A的特征值.
解答:解:因为A-1A=E,所以A=(A-1)-1.
因为|A-1|=-
,所以A=(A-1)-1=
. …(5分)
于是矩阵A的特征多项式为f(λ)=
=λ2-3λ-4,…(8分)
令f(λ)=0,解得A的特征值λ1=-1,λ2=4.…(10分)
因为|A-1|=-
| 1 |
| 4 |
|
于是矩阵A的特征多项式为f(λ)=
|
令f(λ)=0,解得A的特征值λ1=-1,λ2=4.…(10分)
点评:本题考查矩阵的逆矩阵,考查特征值.正确求矩阵的逆矩阵是关键.

练习册系列答案
相关题目
复数
等于( )
| 2+i |
| 1-2i |
A、-
| ||
B、
| ||
| C、-i | ||
| D、i |
在平面直角坐标系中,曲线C:x2-y2=36经过伸缩变换
后,所得曲线的焦点坐标为( )
|
A、(0,±
| ||
B、(±
| ||
C、(0,±
| ||
D、(±
|
已知f(x)为偶函数,当x≥0时,f(x)=2a|x-1|-a,若函数y=f(f(x))恰有10个零点,则a的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、[
|
 ,如果定义了一种运算“
,如果定义了一种运算“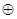 ”,使得集合
”,使得集合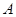 中的元素间满足下列4个条件:
中的元素间满足下列4个条件: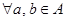 ,都有
,都有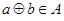 ;
; ,使得对
,使得对 ,都有
,都有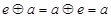 ;
; ,使得
,使得 ;
;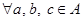 ,都有
,都有 ,
, ”构成“对称集”.
”构成“对称集”. ,运算“
,运算“ ,运算“
,运算“ ,运算“
,运算“