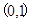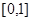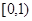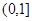题目内容
已知二阶矩阵M有特征值λ=1及对应的一个特征向量e1=
,且M
=
.求矩阵M.
|
|
|
考点:特征值与特征向量的计算
专题:选作题,矩阵和变换
分析:利用待定系数法,结合特征值与特征向量的计算,可得结论.
解答:解:设M=
,
则由
=
,得
再由
=
,得
联立以上方程组解得a=2,b=1,c=0,d=1,
故M=
.…10分.
|
则由
|
|
|
|
再由
|
|
|
|
联立以上方程组解得a=2,b=1,c=0,d=1,
故M=
|
点评:本题考查矩阵的性质和应用、特征值与特征向量的计算,解题时要注意特征值与特征向量的计算公式的运用.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
i为虚数单位,则(
)2014=( )
| 1+i |
| 1-i |
| A、i | B、-1 | C、-i | D、1 |
在极坐标系中,曲线ρ=4cos(θ-
)关于( )
| 5π |
| 6 |
A、直线θ=
| ||
B、直线θ=
| ||
C、点(2,
| ||
| D、极点中心对称 |
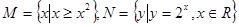 ,则
,则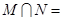 ( )
( )