题目内容
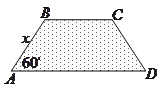
【题目】扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为![]() (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为![]() 平方米,且高度不低于
平方米,且高度不低于![]() 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为![]() (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段![]() 与两腰长的和)为
与两腰长的和)为![]() (米).
(米).
⑴求![]() 关于
关于![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过![]() 米,则其腰长
米,则其腰长![]() 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长![]() 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)外周长的最小值为
;(3)外周长的最小值为![]() 米,此时腰长为
米,此时腰长为![]() 米.
米.
【解析】
试题(1)将梯形高、上底和下底用![]() 或
或![]() 表示,根据梯形面积的计算得到
表示,根据梯形面积的计算得到![]() 和
和![]() 的等式,从而解出
的等式,从而解出![]() ,使问题得以解答,但不要忘记根据题目条件确定函数的定义域;(2)由(1)可得
,使问题得以解答,但不要忘记根据题目条件确定函数的定义域;(2)由(1)可得![]() ,解这个不等式的同时不要忽略了函数的定义域就可得到结果;(3)即求(1)中函数的最小值,可以用导数判断函数的单调性后再求解,也可利用基本不等式求最小值.
,解这个不等式的同时不要忽略了函数的定义域就可得到结果;(3)即求(1)中函数的最小值,可以用导数判断函数的单调性后再求解,也可利用基本不等式求最小值.
试题解析:⑴![]() ,其中
,其中![]() ,
,![]() ,
,
∴![]() ,得
,得![]() , 由
, 由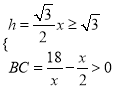 ,得
,得![]()
∴![]() ; 6分
; 6分
⑵![]() 得
得![]() ∵
∵![]() ∴腰长
∴腰长![]() 的范围是
的范围是![]() 10分
10分
⑶![]() ,当并且仅当
,当并且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
∴外周长的最小值为![]() 米,此时腰长为
米,此时腰长为![]() 米. 16分
米. 16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目