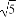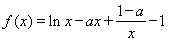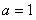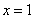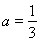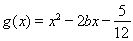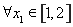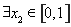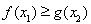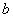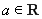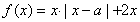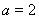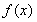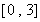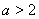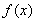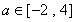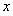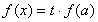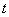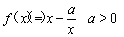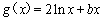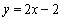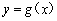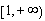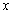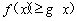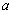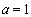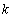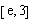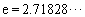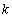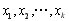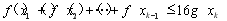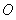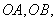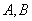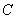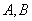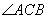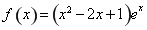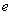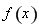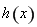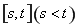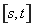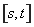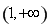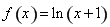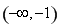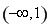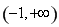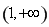题目内容
若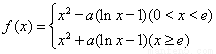 ,其中
,其中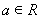 .
.
(1)当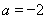 时,求函数
时,求函数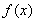 在区间
在区间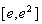 上的最大值;
上的最大值;
(2)当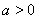 时,若
时,若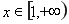 ,
,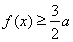 恒成立,求
恒成立,求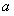 的取值范围.
的取值范围.
(1)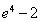 (2)
(2)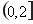
【解析】(1)当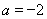 ,
,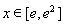 时,
时,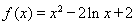 , (1分)
, (1分)
∵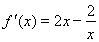 ,∴当
,∴当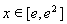 时,
时,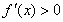 ,(2分)
,(2分)
∴函数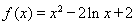 在
在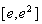 上单调递增, (3分)
上单调递增, (3分)
故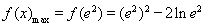
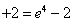 (4分)
(4分)
(2)①当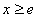 时,
时, ,
,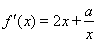 ,
,
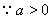 ,
,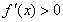 ,∴f(x)在
,∴f(x)在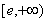 上增函数,(5分)
上增函数,(5分)
故当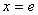 时,
时,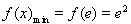 ;(6分)
;(6分)
②当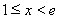 时,
时,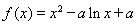 ,
,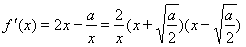 ,(7分)
,(7分)
(i)当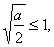 即
即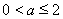 时,
时,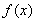 在区间
在区间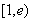 上为增函数,
上为增函数,
当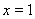 时,
时,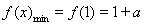 ,且此时
,且此时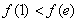
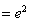 ;(8分)
;(8分)
(ii)当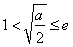 ,即
,即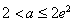 时,
时,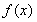 在区间
在区间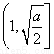 上为减函数,在区间
上为减函数,在区间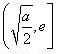 上为增函数,
上为增函数,
故当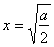 时,
时,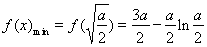 ,且此时
,且此时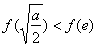
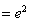 ;(10分)
;(10分)
(iii)当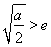 ,即
,即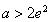 时,
时,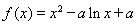 在区间[1,e]上为减函数,
在区间[1,e]上为减函数,
故当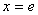 时,
时,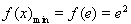 .(11分)
.(11分)
综上所述,函数 的在
的在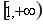 上的最小值为
上的最小值为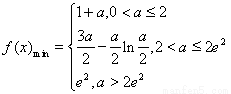 (12分)
(12分)
由 得
得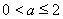 ;由
;由 得无解;
得无解;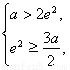 得无解;(13分)
得无解;(13分)
故所求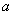 的取值范围是
的取值范围是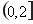 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目