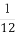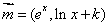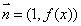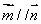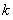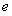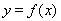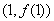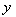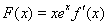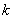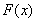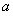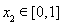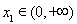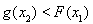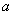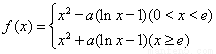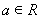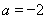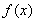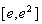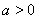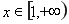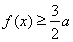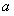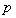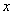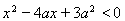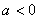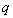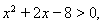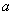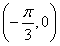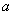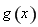题目内容
已知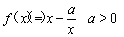 ,
,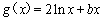 ,且直线
,且直线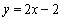 与曲线
与曲线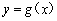 相切.
相切.
(1)若对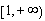 内的一切实数
内的一切实数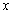 ,不等式
,不等式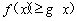 恒成立,求实数
恒成立,求实数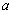 的取值范围;
的取值范围;
(2)当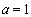 时,求最大的正整数
时,求最大的正整数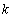 ,使得对
,使得对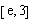 (
(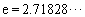 是自然对数的底数)内的任意
是自然对数的底数)内的任意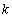 个实数
个实数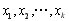 都有
都有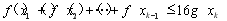 成立;
成立;
(3)求证: .
.
(1)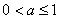 (2)见解析(3)见解析
(2)见解析(3)见解析
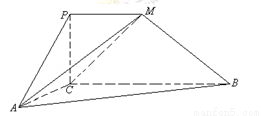
【解析】(1)设点 为直线
为直线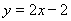 与曲线
与曲线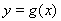 的切点,则有
的切点,则有 .(*)
.(*)
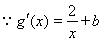 ,
,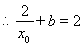 . (**)
. (**)
由(*)、(**)两式,解得 ,
, .……………………………2分
.……………………………2分
由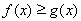 整理,得
整理,得 ,
,
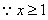 ,
, 要使不等式
要使不等式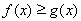 恒成立,必须
恒成立,必须 恒成立.
恒成立.
设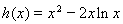 ,
,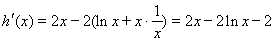 ,
,
 ,
, 当
当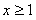 时,
时,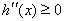 ,则
,则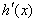 是增函数,
是增函数,
 ,
,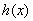 是增函数,
是增函数, ,
, .…………………5分
.…………………5分
因此,实数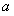 的取值范围是
的取值范围是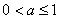 .………………………………………6分
.………………………………………6分
(2)当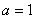 时,
时,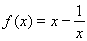 ,
,
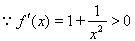 ,
, 在
在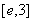 上是增函数,
上是增函数,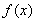 在
在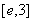 上的最大值为
上的最大值为 .
.
要对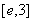 内的任意
内的任意 个实数
个实数 都有
都有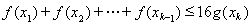
成立,必须使得不等式左边的最大值小于或等于右边的最小值,
 当
当 时不等式左边取得最大值,
时不等式左边取得最大值, 时不等式右边取得最小值.
时不等式右边取得最小值.
 ,解得
,解得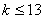 .
.
因此,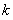 的最大值为
的最大值为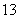 .………………………………………10分
.………………………………………10分
(3)证明(法一):当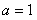 时,根据(1)的推导有,
时,根据(1)的推导有, 时,
时,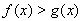 ,
,
即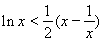 .………………………………………………………11分
.………………………………………………………11分
令 ,得
,得 ,
,
化简得 ,………………………………13分
,………………………………13分
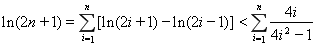 .………………………14分
.………………………14分
(法二)数学归纳法:当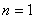 时,左边=
时,左边= ,右边=
,右边=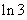 ,
,
根据(1)的推导有, 时,
时, ,即
,即 .
.
令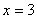 ,得
,得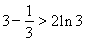 ,即
,即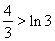 .
.
因此,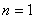 时不等式成立.………………………………11分
时不等式成立.………………………………11分
(另【解析】 ,
,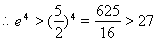 ,
, ,即
,即 .)
.)
假设当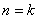 时不等式成立,即
时不等式成立,即 ,
,
则当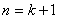 时,
时, ,
,
要证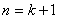 时命题成立,即证
时命题成立,即证 ,
,
即证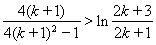 .
.
在不等式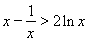 中,令
中,令 ,得
,得
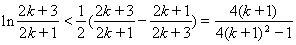 .
.
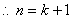 时命题也成立.………………………………………13分
时命题也成立.………………………………………13分
根据数学归纳法,可得不等式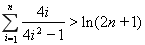 对一切
对一切 成立. …14分
成立. …14分
本题主要考查函数的性质、导数运算法则、导数的几何意义及其应用、不等式的求解与证明、数学归纳法等综合知识,考查学生的计算推理能力及分析问题、解决问题的能力及创新意识.

练习册系列答案
相关题目