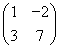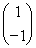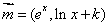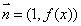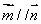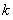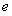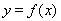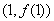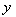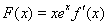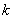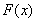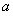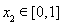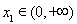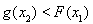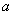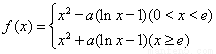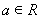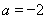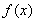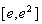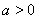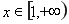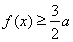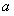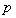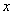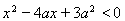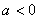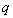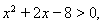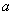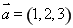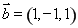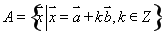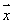题目内容
设函数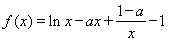 .
.
(Ⅰ)当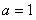 时,求曲线
时,求曲线 在
在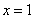 处的切线方程;
处的切线方程;
(Ⅱ)当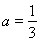 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数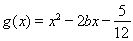 ,若对于
,若对于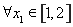 ,
,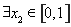 ,使
,使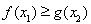 成立,求实数
成立,求实数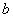 的取值范围.
的取值范围.
(Ⅰ) 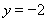 (Ⅱ) 函数
(Ⅱ) 函数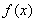 的单调递增区间为
的单调递增区间为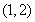 ;单调递减区间为
;单调递减区间为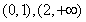 (Ⅲ)
(Ⅲ) 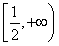
【解析】函数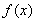 的定义域为
的定义域为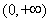 ,
,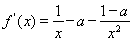 …………2分
…………2分
(Ⅰ)当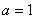 时,
时,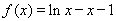 ,
,
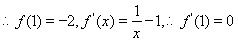 ∴
∴ 在
在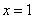 处的切线方程为
处的切线方程为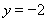 ………5分
………5分
(Ⅱ) 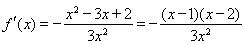
所以当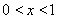 ,或
,或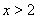 时,
时,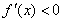 ,当
,当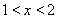 时,
时,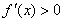
故当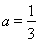 时,函数
时,函数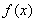 的单调递增区间为
的单调递增区间为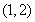 ;
;
单调递减区间为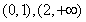 …………8分
…………8分
(Ⅲ)当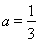 时,由(Ⅱ)知函数
时,由(Ⅱ)知函数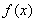 在区间
在区间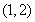 上为增函数,
上为增函数,
所以函数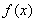 在
在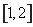 上的最小值为
上的最小值为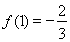
若对于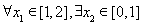 使
使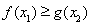 成立
成立
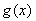 在
在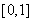 上的最小值不大于
上的最小值不大于 在[1,2]上的最小值
在[1,2]上的最小值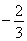 (*)…………10分
(*)…………10分
又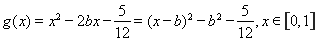
①当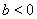 时,
时,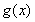 在上
在上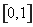 为增函数,
为增函数,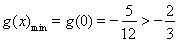 与(*)矛盾
与(*)矛盾
②当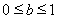 时,
时,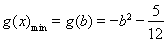 ,
,
由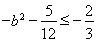 及
及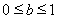 得,
得,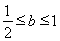 …………12分
…………12分
③当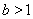 时,
时,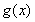 在上
在上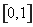 为减函数,
为减函数,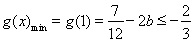 , 此时
, 此时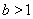
综上所述,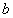 的取值范围是
的取值范围是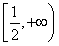 …………14分
…………14分

练习册系列答案
相关题目
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| 物理 成绩好 | 物理 成绩不好 | 合计 |
数学成绩好 | 62 | 23 | 85 |
数学成绩不好 | 28 | 22 | 50 |
合计 | 90 | 45 | 135 |
那么有把握认为数学成绩与物理成绩之间有关的百分比为( )
(A)25% (B)75% (C)95% (D)99%