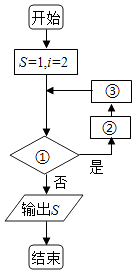
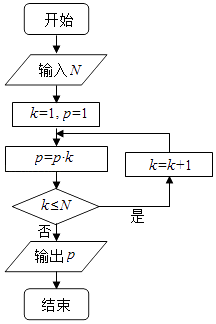
题目内容
【题目】已知函数f(x)=2x- ![]() 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(1)当a=1时,求函数y=f(x)的值域;
(2)求函数y=f(x)在区间(0,1]上的最大值及最小值,并求出当函数f(x)取得最值时x的值.
【答案】
(1)解:当a=1时,f(x)=2x- ![]() ,任取1≥x1>x2>0,
,任取1≥x1>x2>0,
则f(x1)-f(x2)=2(x1-x2)- ![]() =(x1-x2)
=(x1-x2) ![]() .
.
∵1≥x1>x2>0,∴x1-x2>0,x1x2>0.
∴f(x1)>f(x2),∴f(x)在(0,1]上单调递增,无最小值,当x=1时取得最大值1,所以f(x)的值域为(-∞,1].
(2)解:当a≥0时,y=f(x)在(0,1]上单调递增,无最小值,当x=1时取得最大值2-a;
当a<0时,f(x)=2x+ ![]() ,
,
当 ![]() ≥1,即a∈(-∞,-2]时,y=f(x)在(0,1]上单调递减,无最大值,当x=1时取得最小值2-a;
≥1,即a∈(-∞,-2]时,y=f(x)在(0,1]上单调递减,无最大值,当x=1时取得最小值2-a;
当 ![]() <1,即a∈(-2,0)时,y=f(x)在
<1,即a∈(-2,0)时,y=f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]()
上单调递增,无最大值,当x= ![]() 时取得最小值2
时取得最小值2 ![]() .
.
【解析】本题主要考查求解函数的值域以及最值问题。(1)利用函数的单调性求函数的值域问题。(2)根据函数的单调性求函数在区间上的最值问题。

【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取 ![]() 名同学(男
名同学(男 ![]() 人,女
人,女 ![]() 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
附表及公式: ![]()

(1)能否据此判断有 ![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的 ![]() 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为
名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ![]() ,求
,求 ![]() 的分布列和
的分布列和 ![]() .
.