Question

（2011•自贡三模）给出下列5个命题：
①0＜a≤

1

5

是函数f（x）=ax²+2（a-1）x+2在区间（-∞，4]上为单调减函数的充要条件
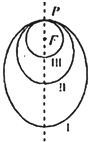
②如图所示，“嫦娥探月卫星”沿地月转移轨道飞向月球，在月球附近一点P进入以月球球心F为一个焦点的椭圆叙道I绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行，若用2c_l和2c₂分别表示椭圆轨道I和II的焦距，用2a1和2a2分别表示椭圆轨道I和II的长轴的长，则有a₁-c₁=a₂-c₂；
③y=f（x）与它的反函数y=f^-1（x）的图象若相交，则交点必在直线y=x上；
④若a∈（π，

5π

4

），则

1

1-tanα

＞1+tanα＞

2tanα

；
⑤函数f（x）=

e-x+3

e-x+2

（e是自然对数的底数）的最小值为2．
其中所有真命题的代号有

②④

．

Answer 1

分析：①利用二次函数的性质，由其在区间（-∞，4]上为单调减函数解出参数的取值范围，依据依据充要条件的定义进行判断即可，
②由椭圆的性质进行判断即可，
③利用特例说明其不成立即可，如指数函数y=(

1

16

)x的图象与对数函数y=log

1

16

x的图象的交点有P（

1

2

，

1

4

），Q（

1

4

，

1

2

），就是不在直线y=x上的两个交点，由此可知原结论不正确，
④由a∈（π，

5π

4

），可知0＜tanα＜1，可得（1-tanα）（1+tan）=1-tan²α＜1，于是

1

1-tanα

＞1+tanα；再根据均值不等式可得1+tanα＞

2tanα

，
⑤由均值不等式可判断出不存在实数x使得等号成立，故函数f（x）不存在最小值．

解答：解：对于①：函数f（x）=ax²+2（a-1）x+2在区间（-∞，4]上为单调减函数，若a=0时成立，若a＞0时，必有-

a-1

a

≥4解得a≤

1

5

，故可得出0≤a≤

1

5

，由此知①中的条件与结论之间是充分不必要条件．故不是真命题；
②由椭圆的性质知a₁-C_l=a₂-c₂，即有a₂+C_l=a₁+c₂，此四数构成一个等差数列，由基本不等式得c₁a₂＞a₁c₂，故是真命题；
③指数函数y=(

1

16

)x的图象与对数函数y=log

1

16

x的图象的交点有P（

1

2

，

1

4

），Q（

1

4

，

1

2

），就是不在直线y=x上的两个交点，故不是真命题；
④∵由a∈（π，

5π

4

），可知0＜tanα＜1，可得（1-tanα）（1+tan）=1-tan²α＜1，再根据均值不等式可得1+tanα＞

2tanα

，则

1

1-tanα

＞1+tanα＞

2tanα

，故是真命题；
⑤由均值不等式函数f（x）=f（x）=

e-x+3

e-x+2

=

e-x+2

+

1

e-x+2

≥2，由e^-x+2=1知不存在实数x使得等号成立，故函数f（x）不存在最小值，故不是真命题．
故答案为：②④．

点评：本题作为一个判断命题真假的题目，涉及到了函数的单调性椭圆的性质等内容，题目较难判断，每一个知识点都是高考中比较重要的，从中总结下对命题的考试与这些知识的衔接．综合考查了函数的单调性、最值，均值不等式，反函数等有关知识，对学生要求较高．属于难题．