题目内容
1．函数f（x）=x2-2x+2在区间[t，t+1]上的最小值为g（t），求g（t）的表达式及其最值．分析 先求出函数的对称轴，通过讨论t的范围，确定函数的单调性，从而求出g（t）的表达式，画出g（t）的图象，得到最值即可．
解答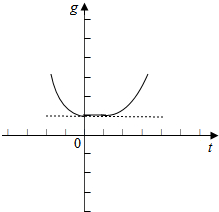 
解：函数f（x）的对称轴是x=1，
∴函数f（x）在（-∞，1）单调递减，在（1，+∞）单调递增，
①当t+1≤1，即t≤0时，f（x）在[t，t+1]单调递减，
g（t）=f（x）min=f（t+1）=t2+1，
②1＜t+1＜2，即0＜t＜1时，f（x）在[t，1）递减，在（1，t+1]递增，
∴g（t）=f（x）min=f（1）=1，
③t≥1时，函数f（x）在[t，t+1]单调递增，
∴g（t）=f（x）min=f（t）=t2-2t+2，
∴g（t）=$\left\{\begin{array}{l}{{t}^{2}+1，（t≤0）}\\{1，（0＜t＜1）}\\{{t}^{2}-2t+2（t≥1）}\end{array}\right.$，
画出函数g（t）的图象，如图示：
∴g（t）的最小值是1，无最大值．
点评 本题考查了二次函数的性质，函数的单调性、最值问题，考查分类讨论思想，是一道中档题．
练习册系列答案
相关题目
9．下列结论中正确的是（ ）
| A． | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$与$\overrightarrow{b}$的长度相等且方向相同或相反 | |
| B． | 若向量$\overrightarrow{AB}$与$\overrightarrow{CD}$满足|$\overrightarrow{AB}$|＞|$\overrightarrow{CD}$|，且$\overrightarrow{AB}$与$\overrightarrow{CD}$同向，则$\overrightarrow{AB}$＞$\overrightarrow{CD}$ | |
| C． | 若$\overrightarrow{a}$=$\overrightarrow{b}$，则$\overrightarrow{a}$∥$\overrightarrow{b}$ | |
| D． | 由于零向量方向不定，故零向量不能与任一向量平行 |