题目内容
3.若函数f(x)=lnx+x+$\frac{2}{x}$-a有零点,则a的取值范围是[3,+∞).分析 由f(x)=0得a=lnx+x+$\frac{2}{x}$,构造函数g(x)=lnx+x+$\frac{2}{x}$,利用导数,求函数的极值即可得到结论.
解答 解:f(x)=lnx+x+$\frac{2}{x}$-a=0得a=lnx+x+$\frac{2}{x}$,
设g(x)=lnx+x+$\frac{2}{x}$,则函数的定义域为(0,+∞),
则函数的导数g′(x)=$\frac{1}{x}+1-\frac{2}{{x}^{2}}$,
由g′(x)=$\frac{1}{x}+1-\frac{2}{{x}^{2}}$=0,得$\frac{2}{{x}^{2}}$-$\frac{1}{x}$-1=0,
即($\frac{1}{x}$-1)($\frac{2}{x}$+1)=0
∵x>0,∴$\frac{2}{x}$>0,
∴$\frac{1}{x}$-1=0,即$\frac{1}{x}$=1,解得x=1.
当0<x<1时,g′(x)<0,此时函数g(x)递减,
当x>1时,g′(x)>0,此时函数g(x)递增,
即当x=1时,函数g(x)取得极小值,g(1)=ln1+1+2=3,
即g(x)≥3,
若函数f(x)=lnx+x+$\frac{2}{x}$-a有零点,即方程g(x)=lnx+x+$\frac{2}{x}$=a有解,
即a≥3,
故a的取值范围是[3,+∞),
故答案为:[3,+∞)
点评 本题主要考查函数零点的意义,构造函数,利用导数求出函数的最值是解决本题的关键.综合性较强.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
13.将函数y=sin(2x-$\frac{π}{3}$)的图象向右平移$\frac{7π}{12}$个单位,再将图象上每个点的横坐标扩大到原来的2倍,纵坐标不变,得到的图象对应的函数表达式是( )
| A. | y=sin(x+$\frac{5}{6}$π) | B. | y=cosx | C. | y=sin(4x+$\frac{5}{6}$π) | D. | y=cos4x |
18.在△ABC中,若2b=a+c,b2=ac,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
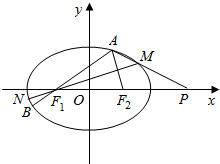 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆C上一动点(A异于左、右顶点),F1、F2分别为椭圆C的左、右焦点,且△AF1F2面积的最大值为1;
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆C上一动点(A异于左、右顶点),F1、F2分别为椭圆C的左、右焦点,且△AF1F2面积的最大值为1;