题目内容
19．函数f（x）满足f（x）•f（x+2）=13，若f（1）=2，则f（99）=$\frac{13}{2}$．分析 由已知f（x）•f（x+2）=13得f（x+4）=f（x），根据周期函数的定义判断出函数的周期，可得f（99）=f（-1），再利用已知条件求出即可．
解答 解：由f（x）•f（x+2）=13得，f（x+2）f（x+4）=13，
即f（x）=f（x+4），
所以函数f（x）是周期为4的周期函数．
所以f（99）=f（25×4-1）=f（-1）．
由f（-1）•f（1）=13，f（1）=2，得f（-1）=$\frac{13}{2}$，
所以f（99）=$\frac{13}{2}$，
故答案为：$\frac{13}{2}$．
点评 本题考查了函数的周期性的应用，求出函数的周期是解题的关键，属于基础题．
练习册系列答案
相关题目
10．在△ABC中，若a+c=2b，则有（ ）
| A． | 60°≤B≤90° | B． | 0°＜B≤60° | C． | 90°≤B≤120° | D． | 120°≤B≤180° |
8．某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
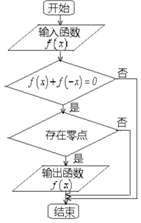
| A． | f（x）=$\frac{|x|}{x}$ | B． | f（x）=$\frac{cosx}{x}$（-$\frac{π}{2}$＜x＜$\frac{π}{2}$） | ||
| C． | f（x）=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | D． | f（x）=x2ln（x2+1） |