题目内容
已知f(x)=x2–2x+3,g(x)=kx–1,则“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 ( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:要是f(x)≥g(x)在R上恒成立,需x2–2x+3≥kx–1,即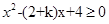 在R上恒成立,所以
在R上恒成立,所以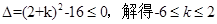 ,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
考点:二次函数的性质;充分、必要、充要条件的判断。
点评:若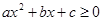
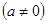 恒成立
恒成立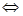
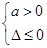 ;若
;若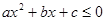
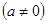 恒成立
恒成立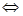
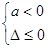 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
a<0是方程 至少有一个负数根的( )
至少有一个负数根的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“若α= ,则tanα=1”的逆否命题是( )
,则tanα=1”的逆否命题是( )
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
已知命题p: ,则命题p的否定是( )
,则命题p的否定是( )
A.不存在 | B. |
C. | D. |
“双曲线的方程为 ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题:“若 ,则
,则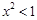 ”的逆否命题是( )
”的逆否命题是( )
A.若 则 则 | B.若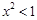 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知 为两个命题,则“
为两个命题,则“ 是真命题”是 “
是真命题”是 “ 是真命题”的( )
是真命题”的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
设甲:函数 的值域为
的值域为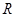 ,乙:函数
,乙:函数 有四个单调区间,那么甲是乙的
有四个单调区间,那么甲是乙的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设命题 :
: ,命题
,命题 :一元二次方程
:一元二次方程 有实数解.则
有实数解.则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |