��Ŀ����
3�� ��һ�ζ�ij��42��ѧ���μӿ�������������ȤС�飨ÿ�˲μ���ֻ�μ�һ����ȤС�飩��������У���ͳ�Ƶõ�����2��2������������λ���ˣ�
��һ�ζ�ij��42��ѧ���μӿ�������������ȤС�飨ÿ�˲μ���ֻ�μ�һ����ȤС�飩��������У���ͳ�Ƶõ�����2��2������������λ���ˣ�| ���� | ���� | �ܼ� | |
| ��ͬѧ | 16 | 6 | 22 |
| Ůͬѧ | 8 | 12 | 20 |
| �ܼ� | 24 | 18 | 42 |
��2����������ݻ����������ĵȸ�����ͼ����ͨ������ͼ�жϲμӡ�����С�顱������С�顱���Ա��Ƿ��йأ�
��3��������������ݣ��ж��Ƿ���95%�İ�����Ϊ�μӡ�����С�顱������С�顱���Ա��йأ�
�����ٽ�ֵ�����ο���
| P��k2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k2 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1������2��2�����������Ƹð�ͬѧ�У��μ�������ȤС���ͬѧ�ı�����
��2���������ݻ����������ĵȸ�����ͼ�������жϲμӡ�����С�顱������С�顱���Ա��Ƿ��йأ�
��3�����k2�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
��� �⣺��1���ð42�ˣ��μ�������ȤС�����18�ˣ����Ա���$\frac{18}{42}=\frac{3}{7}$-------------------��4�֣���
��2����ͼ��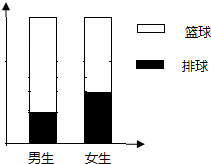
�μӡ�����С�顱������С�顱���Ա��й�--------------------------------��8�֣�
��3��k2=$\frac{504}{110}��4.582��3.841$��
������95%�İ�����Ϊ�μӡ�����С�顱������С�顱���Ա��й�--��12�֣�
���� ���⿼���������Ķ����Լ��飬�ȸ�����ͼ�ȣ�����ѧ�����������������������е��⣮

��ϰ��ϵ�д�
 ����5��2���ϵ�д�
����5��2���ϵ�д�
�����Ŀ
17��2005��ij�еĿ�������״���ֲ������
����X��50ʱ����������Ϊ�ţ�50��X��100ʱ��������Ϊ����100��X��150ʱ����������Ϊ����Ⱦ��
��1����E��X����ֵ��
��2������������ﵽ�Ż����ĸ��ʣ�
| ��Ⱦָ��X | 30 | 60 | 100 | 110 | 130 | 140 |
| P | $\frac{1}{10}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{7}{30}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
��1����E��X����ֵ��
��2������������ﵽ�Ż����ĸ��ʣ�
8��������f��x��=loga��$\frac{{x}^{2}+a}{x}$������Сֵ1����a���ڣ�������
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | 2 | D�� | 4 |
15����a��b��������a��b����$P=\frac{a}{b}$��$Q=\frac{a+m}{b+m}$��m��0����������
| A�� | P=Q | B�� | P��Q | ||
| C�� | P��Q | D�� | P��Q��С��ϵ��ȷ�� |
11����֪����z=1+i��iΪ������λ����z2=��������
| A�� | 2+2i | B�� | 2i | C�� | 2-2i | D�� | -2i |
11����ʵ����Χ�ڣ����в��ȹ�ϵ����������ǣ�������
| A�� | x2��0 | B�� | a2+b2��2ab | C�� | x+1��x | D�� | |x+1|��|x| |