题目内容
【题目】已知长方形ABCD如图1中,AD= ![]() ,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.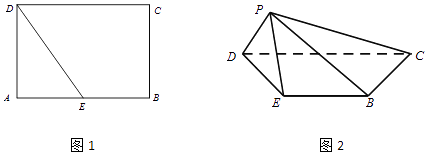
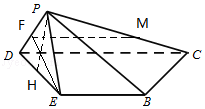
(Ⅰ)若点M为PC中点,求证:BM∥平面PDE;
(Ⅱ)当平面PDE⊥平面BCDE时,求三棱锥E﹣PCD的体积.
【答案】解:证明:(Ⅰ)取DP中点F,连结EF、FM,
∵△PDC中,点F、M分别是DP、PC的中点,
∴FM ![]() DC,又EB
DC,又EB ![]() DC,
DC,
∴FM ![]() EB,∴FEBM是平行四边形,∴BM∥EF,
EB,∴FEBM是平行四边形,∴BM∥EF,
又EF平面PDE,BM平面PDE,
∴BM∥平面PDE.
(Ⅱ)解:∵平面PDE⊥平面EBCD,且平面PDE∩平面EBCD=DE,
过P作PH⊥DE于H,∴PH⊥平面EBCD,
在Rt△PDE中,过P作PH⊥DE于H,∴PH⊥平面EBCD,
在Rt△PDE中,由题意得PH= ![]() ,
,
在Rt△DEC中,DE= ![]() =2,且DE=EC=2,
=2,且DE=EC=2,
∴ ![]() =
= ![]() ,
,
∴三棱锥E﹣PCD的体积VE﹣PCD=VP﹣DEC= ![]() =
= ![]() =
= ![]() .
.
【解析】(Ⅰ)取DP中点F,连结EF、FM,推导出FEBM是平行四边形,从而BM∥EF,由此能证明BM∥平面PDE.(Ⅱ)过P作PH⊥DE于H,则PH⊥平面EBCD,三棱锥E﹣PCD的体积VE﹣PCD=VP﹣DEC , 由此能求出结果.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目