Question

【题目】在边长为1的正方体中，E，F，G，H分别为A1B1 ， C1D1 ， AB，CD的中点，点P从G出发，沿折线GBCH匀速运动，点Q从H出发，沿折线HDAG匀速运动，且点P与点Q运动的速度相等，记E，F，P，Q四点为顶点的三棱锥的体积为V，点P运动的路程为x，在0≤x≤2时，V与x的图象应为（　　）

A.
B.
C.
D.

Answer 1

【答案】C
【解析】（1）当0时，点P与点Q运动的速度相等根据下图得出：面OEF把几何体PEFQ分割为相等的几何体，
∵ ， P到面OEF的距离为x，


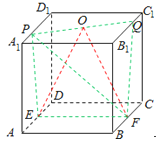
（2）当时，P在AB上，Q在C1D1上，P到 ，
VPEFQ=2VP﹣OEF=2×=定值．
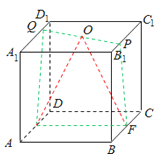
（3）当＜x≤2时，S△OEF= ， P到面OEF的距离为2﹣x，
VPEFQ=2VP﹣OEF=2× ，

V=
故选：C
【考点精析】掌握棱柱的结构特征是解答本题的根本，需要知道两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．