题目内容
(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为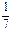 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,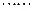 ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
(1)则袋中原有白球的个数;
(2)取球2次终止的概率;
(3)甲取到白球的概率
解:(1)(设袋中原有 个白球,由题意知
个白球,由题意知 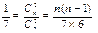
所以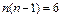 ,解得
,解得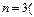 舍去
舍去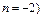 .即袋中原有3个白球. …………………4分
.即袋中原有3个白球. …………………4分
(2)记“取球2次终止”的事件为A. 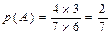 …………………8分
…………………8分
(3)记“甲取到白球”的事件为B,“第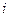 次取到的球是白球”的事件为
次取到的球是白球”的事件为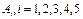 ,因为甲先取,所以甲只有可能在第1次、第3次和第5次取球,则
,因为甲先取,所以甲只有可能在第1次、第3次和第5次取球,则 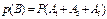 .
.
因为事件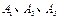
 两两互斥,所以
两两互斥,所以 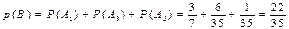 …………………………………12分
…………………………………12分
解析

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为 (
( 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为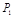 、
、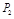 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
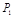 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
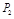 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是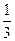 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求: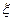 的分布列和数学期望.
的分布列和数学期望. ,乙投篮命中的概率为
,乙投篮命中的概率为 .
. 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.