题目内容
在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为 (
( 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为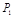 、
、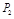 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
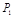 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
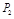 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
(Ⅰ) (Ⅱ)
(Ⅱ)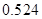 ,2号射箭运动员的射箭水平高.理由见解析。
,2号射箭运动员的射箭水平高.理由见解析。
解析

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 | 射手乙 | ||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 |
| 概率 |  |  |  | 概率 |  |  |  |
(Ⅱ)若两个射手各射击1次,记所得的环数之和为
 ,求
,求 的分布列和期望.
的分布列和期望.  分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 。
。 ,笔试考试成绩每次合格的概率均为
,笔试考试成绩每次合格的概率均为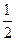 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响.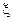 ,求参加考试次数
,求参加考试次数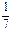 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取, ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求: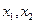 ,记
,记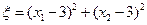 .
.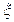 取得最大值和最小值时的概率; (2)
取得最大值和最小值时的概率; (2) 求
求
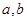 .
.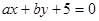 与圆
与圆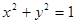 相切的概率;
相切的概率;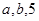 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.