题目内容
已知盘中有编号为A,B,C,D的4个红球,4个黄球,4个白球(共 12个球)现从中摸出4个球(除编号与颜色外球没有区别) (12分)
(1)求掐好包含字母A, B,C,D的概率;
(2)设摸出的4个球中出现的颜色种数为随机变量X.求X的分布列和期望E(X).
(1)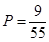 ;(2)分布列见解析,期望
;(2)分布列见解析,期望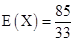 .
.
解析试题分析:(1)按分步乘法原理,可求出恰好包含字母A, B,C,D的事件个数为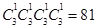 ,从12个球中摸出4个球的个数为
,从12个球中摸出4个球的个数为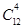 ,相除可得概率;(2)摸出的4个球中出现的颜色种数为随机变量X,可能取值为
,相除可得概率;(2)摸出的4个球中出现的颜色种数为随机变量X,可能取值为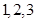 分别求出概率,列出分布列,进一步求出期望.
分别求出概率,列出分布列,进一步求出期望.
试题解析:(Ⅰ) P=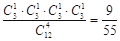 --------------4分
--------------4分
(2)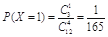 ,
,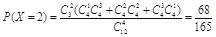 ,
, 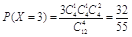 .
.
分布列为:X 1 2 3 P 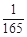
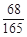
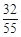
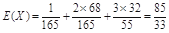 12分
12分
考点:分步乘法原理,离散型随机变量的分布列,离散型随机变量的期望.

练习册系列答案
相关题目
阅读右图的程序框图,则输出S=( )
| A.14 | B.20 | C.30 | D.55 |
执行如图所示的程序框图,如果输入 ,则输出的
,则输出的 的值为
的值为
| A.7 | B.9 | C.2 | D.13 |
将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同的分法种数有( )
| A.2610 | B.720 | C.240 | D.120 |
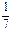 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,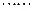 ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求: 的结果是( )
的结果是( )




 ,则输出
,则输出 的值为( )
的值为( )