题目内容
1.已知[x]表示不超过实数x的最大整数(x∈R),如:[-1.3]=-2,[0.8]=0,[3.4]=3.定义{x}=x-[x],求{$\frac{2013}{2014}$}+{$\frac{201{3}^{2}}{2014}$}+{$\frac{201{3}^{3}}{2014}$}+…+{$\frac{201{3}^{2014}}{2014}$}=1007.分析 利用新定义,代入计算,找出规律,可得结论.
解答 解:{$\frac{2013}{2014}$}=$\frac{2013}{2014}$-0=$\frac{2013}{2014}$,
{$\frac{201{3}^{2}}{2014}$}={$\frac{(201{4-1)}^{2}}{2014}$}
={$\frac{201{4}^{2}-2×2014+1}{2014}$}
={2012+$\frac{1}{2014}$}
=2012+$\frac{1}{2014}$-[2012+$\frac{1}{2014}$]
=$\frac{1}{2014}$,
{$\frac{201{3}^{3}}{2014}$}={$\frac{{(2014-1)}^{3}}{2014}$}=$\frac{2013}{2014}$,{$\frac{201{3}^{4}}{2014}$}={$\frac{{(2014-1)}^{4}}{2014}$}=$\frac{1}{2014}$,
∴指数为奇次幂时,值为$\frac{2013}{2014}$,为偶次幂时,值为$\frac{1}{2014}$
∴原式=1007,
故选:B.
点评 本题考查简单的合情推理,考查新定义,考查学生的计算能力,是中档题础.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
2.log99+log0.21=( )
| A. | 10 | B. | 9 | C. | 2 | D. | 1 |
13.从0,8中任取一数,从3,5,7中任取两个数字组成无重复数字的三位数,其中奇数的个数为( )
| A. | 24 | B. | 18 | C. | 12 | D. | 6 |
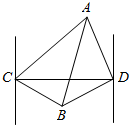 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).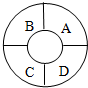 有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.
有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.