题目内容
19.已知点A(5,3),B(-4,10),C(10,6),D(3,-4),求证:AD⊥BC.分析 由已知点的坐标求出$\overrightarrow{AD}、\overrightarrow{BC}$的坐标,再求出其数量积,由数量积等于0得答案.
解答 证明:∵A(5,3),B(-4,10),C(10,6),D(3,-4),
∴$\overrightarrow{AD}=(-2,-7)$,$\overrightarrow{BC}=(14,-4)$,
则$\overrightarrow{AD}•\overrightarrow{BC}=-2×14+(-4)×(-7)=0$.
∴$\overrightarrow{AD}⊥\overrightarrow{BC}$,即AD⊥BC.
点评 本题考查平面向量数量积的坐标表示,考查了向量垂直与数量积间的关系,是基础题.

练习册系列答案
相关题目
9.已知角α、β的终边互为反向延长线,则α-β的终边在( )
| A. | x轴的非负半轴上 | B. | y轴的非负半轴上 | C. | x轴的非正半轴上 | D. | y轴的非正半轴上 |
4.1.2log6$\sqrt{2}$+3log6$\root{3}{3}$=( )
| A. | 0 | B. | 1 | C. | 6 | D. | log6$\frac{2}{3}$ |
18. 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.| A. | n2 | B. | n2+n | C. | 3n2-3n+1 | D. | 3n2-3n |
19.若输出k的值为6,则判断框内可填入的条件是( )
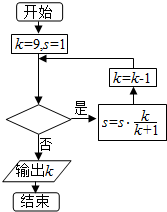

| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |