题目内容
某人上楼梯，每步上一阶的概率为
，每步上二阶的概率为
，设该人从台阶下的平台开始出发，到达第
阶的概率为
.
(1)求
；;
(2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.
，每步上二阶的概率为，设该人从台阶下的平台开始出发，到达第阶的概率为.(1)求
；;(2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.
(1) P2=
×+
；
(2)ξ的分布列为：
=5×()5+6×
。
×+；(2)ξ的分布列为：
| ξ | 5 | 6 | 7 | 8 | 9 | 10 |
| P |  |  |  |  |  |  |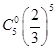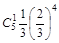
=5×()5+6×。试题分析：(1) 从平台到达第二阶有二种走法：走两步，或一步到达， 2分
故概率为P2=
×+ 6分(2)该人走了五步，共上的阶数ξ取值为5，6，7，8，9，10 .8分
ξ的分布列为：
| ξ | 5 | 6 | 7 | 8 | 9 | 10 |
| P | | | | | | |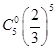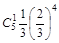
=5×()5+6× 12分点评：中档题，这种类型是近几年高考题中经常出现的，考查离散型随机变量的分布列和期望，大型考试中理科考试必出的一道问题．的计算能力要求较高。
练习册系列答案
相关题目
名志愿者利用周末和节假日参加社会公益活动,活动内容是：1、到各社区宣传慰问,倡导文明新风；2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示：
为选出的4个人中选科目甲的人数，求
（
）个大小相同的球，其中有3个红球和
个白球．已知从
，且
。若有放回地从口袋中连续地取四次球（每次只取一个球），在四次取球中恰好取到两次红球的概率大于
。
为第一次取到白球时的取球次数，求
。
的值.
，则
（ ）
