题目内容
袋中装着标有数字1,2,3,4,5的小球各2个,现从袋中任意取出3个小球,假设每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字分别为1,2,3的概率;
(Ⅱ)求取出的3个小球上的数字恰有2个相同的概率;
(Ⅲ)用X表示取出的3个小球上的最大数字,求 的值.
的值.
(Ⅰ)求取出的3个小球上的数字分别为1,2,3的概率;
(Ⅱ)求取出的3个小球上的数字恰有2个相同的概率;
(Ⅲ)用X表示取出的3个小球上的最大数字,求
 的值.
的值.(Ⅰ)解:记“取出的3个小球上的数字分别为1,2,3”的事件为A, 1分
则
答:取出的3个小球上的数字恰有2个相同的概率为 4分
4分
(Ⅱ)解:记“取出的3个小球上的数字恰有2个相同”的事件为B, 5分
则
答:取出的3个小球上的数字分别为1,2,3的概率为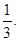 8分
8分
(Ⅲ)解:由题意,X可以取到2,3,4,5,
所以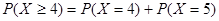 。 9分
。 9分
又因为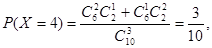 11分
11分
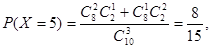
所以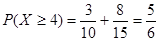 。 13分
。 13分
则

答:取出的3个小球上的数字恰有2个相同的概率为
 4分
4分(Ⅱ)解:记“取出的3个小球上的数字恰有2个相同”的事件为B, 5分
则

答:取出的3个小球上的数字分别为1,2,3的概率为
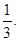 8分
8分(Ⅲ)解:由题意,X可以取到2,3,4,5,
所以
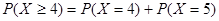 。 9分
。 9分又因为
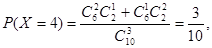 11分
11分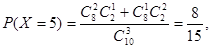
所以
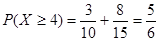 。 13分
。 13分本试题主要是考查了古典概型概率的运用。
(1)先分析整个试验中基本事件数然后分析事件A发生的基本事件数,结合古典概型概率公式得到结论。
(2)记“取出的3个小球上的数字恰有2个相同”的事件为B,利用事件B发生的基本事件数和试验空间的比值得到。
(3)由题意,X可以取到2,3,4,5,那么各个取值的概率值可以解得。相加得到结论。
(1)先分析整个试验中基本事件数然后分析事件A发生的基本事件数,结合古典概型概率公式得到结论。
(2)记“取出的3个小球上的数字恰有2个相同”的事件为B,利用事件B发生的基本事件数和试验空间的比值得到。
(3)由题意,X可以取到2,3,4,5,那么各个取值的概率值可以解得。相加得到结论。

练习册系列答案
相关题目
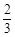 ,现种植这种种子4粒,求:
,现种植这种种子4粒,求: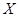 的分布列及平均数.
的分布列及平均数.  ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第 阶的概率为
阶的概率为 .
. ;;
;; =____________.
=____________. 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析,
 项目
项目 (万元)与
(万元)与 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.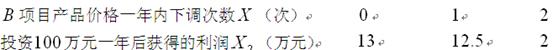
 ;
; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
). 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 的概率;
的概率; 个点,连续取
个点,连续取 次,得到
次,得到 ,求
,求 的分布列和数学期望.
的分布列和数学期望.





