题目内容
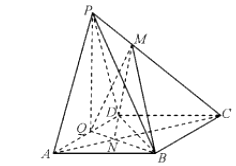
【题目】如图,在四棱锥中P﹣ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形. 
(1)求证:AD⊥PB;
(2)已知点M是线段PC上,MC=λPM,且PA∥平面MQB,求实数λ的值.
【答案】
(1)证明:如图,连结BD,由题意知四边形ABCD为菱形,∠BAD=60°,
∴△ABD为正三角形,
又∵AQ=QD,∴Q为AD的中点,∴AD⊥BQ,
∵△PAD是正三角形,Q为AD中点,
∴AD⊥PQ,又BQ∩PQ=Q,∴AD⊥平面PQB,
又∵PB平面PQB,∴AD⊥PB.
(2)解:连结AC,交BQ于N,连结MN,
∵AQ∥BC,∴ ![]() ,
,
∵PN∥平面MQB,PA平面PAC,
平面MQB∩平面PAC=MN,
∴根据线面平行的性质定理得MN∥PA,
∴ ![]() ,
,
综上,得 ![]() ,∴MC=2PM,
,∴MC=2PM,
∵MC=λPM,∴实数λ的值为2.
【解析】(1)连结BD,则△ABD为正三角形,从而AD⊥BQ,AD⊥PQ,进而AD⊥平面PQB,由此能证明AD⊥PB.(2)连结AC,交BQ于N,连结MN,由AQ∥BC,得 ![]() ,根据线面平行的性质定理得MN∥PA,由此能求出实数λ的值.
,根据线面平行的性质定理得MN∥PA,由此能求出实数λ的值.
【考点精析】认真审题,首先需要了解空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点),还要掌握直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行)的相关知识才是答题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(2)商店记录了50天该商品的日需求量(单位:件),整理得表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间[400,550]”为事件A,求P(A)的估计值.
