题目内容
【题目】已知圆![]() 的圆心为原点,且与直线
的圆心为原点,且与直线![]() 相切.
相切.
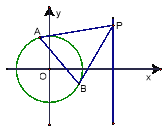
(1)求圆![]() 的方程;
的方程;
(2)点![]() 在直线
在直线![]() 上,过
上,过![]() 点引圆
点引圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题分析:(1)由圆C与直线相切,得到圆心到直线的距离d=r,故利用点到直线的距离公式求出d的值,即为圆C的半径,又圆心为原点,写出圆C的方程即可;(2)由PA,PB为圆O的两条切线,根据切线的性质得到OA与AP垂直,OB与PB垂直,根据90°圆周角所对的弦为直径可得A,B在以OP为直径的圆上,设出P的坐标为(8,b),由P和O的坐标,利用线段中点坐标公式求出OP中点坐标,即为以OP为直径的圆的圆心坐标,利用两点间的距离公式求出OP的长,即为半径,写出以OP为直径的圆方程,整理后,由AB为两圆的公共弦,两圆方程相减消去平方项,得到弦AB所在直线的方程,可得出此直线方程过(2,0),得证
试题解析:(1)依题意得:圆![]() 的半径
的半径![]() ,……………2分
,……………2分
所以圆![]() 的方程为
的方程为![]() 。……………4分
。……………4分
(2)![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]() 。
。
![]() 在以
在以![]() 为直径的圆上。……………6分
为直径的圆上。……………6分
设点![]() 的坐标为
的坐标为![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() 。
。
![]() 以
以![]() 为直径的圆方程为
为直径的圆方程为![]() ……………8分
……………8分
化简得:![]()
![]() 为两圆的公共弦,
为两圆的公共弦,
![]() 直线
直线![]() 的方程为
的方程为![]() ……………10分
……………10分
所以直线![]() 恒过定点
恒过定点![]() 。……………12分
。……………12分

练习册系列答案
相关题目