题目内容
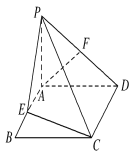
【题目】如图，PA垂直于矩形ABCD所在的平面，E、F分别是AB、PD的中点，∠ADP＝45°.
（1）求证：AF∥平面PCE.
（2）求证：平面PCD⊥平面PCE.
（3）若AD＝2，CD＝3，求点F到平面PCE的距离．
【答案】（1）详见解析（2）详见解析（3）
【解析】
试题分析：（1）关键是证明AF与平面PEC内的一条直线平行，为此可取PC的中点G，论证AF∥EG；（2）可转化为证明线面垂直；（3）可以充分运用（2）的结论，结合线段比例关系求解点F到平面PCE的距离
试题解析：（1）证明：设M为PC中点，连接ME、MF.
则MF∥ 
CD，MF= 
CD，AE∥
CD，AE=
CD
∴MF∥AE，MF=AE∴四边形AEMF为平行四边形．…………2分
∴AF∥ME，又∵ME平面PCE，AF平面PCE
∴AF∥平面PCE. …………4分
（2）证明：∵PA⊥平面ABCD，∠PDA＝45°，
∴△PAD为等腰直角三角形，∵PF＝FD，∴AF⊥PD，又∵PA⊥平面ABCD，PA平面PAD，
∴平面PAD⊥平面ABCD. …………6分
∵平面PAD∩平面ABCD＝AD，
CD⊥AD，CD平面ABCD.
∴CD⊥平面PAD，∴AF⊥CD，
又∵PD∩CD＝D，∴AF⊥平面PCD.
∵EM∥AF，
∴EM⊥平面PCD.
∵EM平面PCE，
∴平面PCE⊥平面PCD. …………8分
（3）过点F作FG⊥PC，交PC于G，∵平面PCE⊥平面PCD，∴FG⊥平面PCE，即FG为点F到平面PCE的距离．…………10分
在Rt△PCD中，PD＝2
，PC＝
.
∵△PFG∽△PCD，∴
，
∴FG＝.…………12分
练习册系列答案
相关题目
