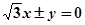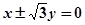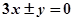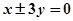题目内容
已知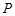 是椭圆
是椭圆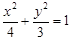 上的一点,
上的一点,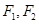 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若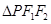 的内切圆半径为
的内切圆半径为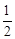 ,则
,则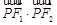 的值为( )
的值为( )
A.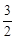 | B.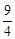 | C.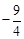 | D. 0 |
B
解析试题分析:因为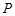 是椭圆
是椭圆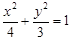 上的一点,所以
上的一点,所以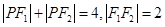 ,由于
,由于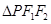 的内切圆半径为
的内切圆半径为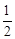 ,所以
,所以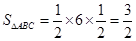 ,
,
而 ,
,
而在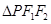 中,利用余弦定理可得
中,利用余弦定理可得 ,
,
两式结合可以求出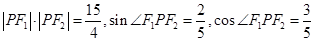 ,
,
所以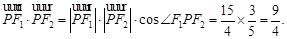
考点:本小题主要考查内切圆半径与三边的关系、椭圆上点的性质、椭圆中基本量之间的运算、三角形面积公式、同角三角函数的基本关系式和余弦定理的综合应用,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:本小题涉及到的知识点较多,要综合运用所学知识才能求解,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,A,B,C分别为 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
A.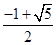 | B.1-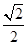 | C.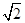 -1 -1 | D.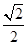 |
已知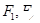 是双曲线的两个焦点,
是双曲线的两个焦点,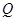 是双曲线上任一点(不是顶点),从某一焦点引
是双曲线上任一点(不是顶点),从某一焦点引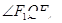 的平分线的垂线,垂足为
的平分线的垂线,垂足为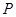 ,则点
,则点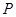 的轨迹是( )
的轨迹是( )
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
已知椭圆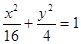 ,过点
,过点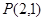 且被点
且被点 平分的椭圆的弦所在的直线方程是( )
平分的椭圆的弦所在的直线方程是( )
A.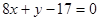 | B.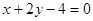 | C.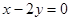 | D.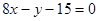 |
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,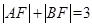 ,则线段AB的中点到y轴的距离为
,则线段AB的中点到y轴的距离为
A.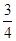 | B.1 | C.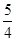 | D.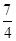 |
椭圆 的两焦点之间的距离为 ( )
的两焦点之间的距离为 ( )
A. | B. | C.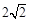 | D. |
双曲线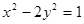 的右焦点的坐标为 ( )
的右焦点的坐标为 ( )
A.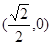 | B.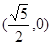 | C.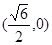 | D.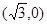 |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
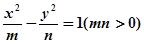 的离心率为2,有一个焦点恰好是抛物线
的离心率为2,有一个焦点恰好是抛物线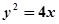 的焦点,则此双曲线的渐近线方程是 ( )
的焦点,则此双曲线的渐近线方程是 ( )