题目内容
17.若x0∈R满足f(x0)=x0,则称x0为f(x)的不动点.(1)若函数f(x)=x2+ax+a没有不动点,求实数a的取值范围;
(2)若函数f(x)=-lnx+3的不动点x0∈[n,n+1],n∈Z,求n的值;
(3)若函数f(x)=log2(4x+a•2x+a+1)有不动点,求实数a的取值范围.
分析 (1)不动点实际上就是方程f(x0)=x0的实数根.二次函数f(x)=x2+ax+a没有不动点,是指方程x=x2+ax+a无实根.即方程x=x2+ax+a无实根,然后根据根的判别式△<0解答即可.
(2)先转化为两个简单函数判断交点所在区间的大致范围,再由零点判定定理确定即可.
(3)函数f(x)=log2(4x+a•2x+a+1)有不动点,转化为关于2x的方程4x+(a-1)•2x+a+1=0,有正解,得到不等式求解即可.
解答 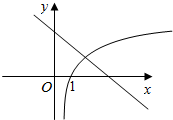 解:(1)根据题意,得x=x2+ax+a无实数根,
解:(1)根据题意,得x=x2+ax+a无实数根,
即x2+(a-1)x+a=0无实数根,
∴△=(a-1)2-4a<0,
解得:3-$2\sqrt{2}$<a<3+2$\sqrt{2}$;
故答案为:(3-$2\sqrt{2}$,3+2$\sqrt{2}$).
(2)解:函数f(x)=-lnx+3的不动点x0∈[n,n+1],n∈Z,即lnx+x-3=0
∴lnx=3-x,令g(x)=lnx,h(x)=3-x在同一坐标系画出图象可得
由图可知x0>1,令f(x)=lnx+x-3,
∵f(1)f(2)=-2(ln2-2)>0,
f(2)f(3)=(ln2-2)ln3<0,
f(3)f(4)=ln3(ln4+1)>0,
可知n=2,
(3)函数f(x)=log2(4x+a•2x+a+1)有不动点,可得log2(4x+a•2x+a+1)=x,
转化为关于2x的方程4x+(a-1)•2x+a+1=0有正根,令t=2x.可得t2+(a-1)t+a+1=0,
$\left\{\begin{array}{l}△={(a-1)}^{2}-4a-4≥0\\ a-1<0\end{array}\right.$或a+1<0,
解得:a<1.
点评 本题主要考查函数零点所在区间的求法--图象法和零点判定定理.将函数的零点问题转化为两个函数交点的问题是常用的手段.二次函数图象上点的坐标特征、函数与方程的综合运用,解答该题时,借用了一元二次方程的根的判别式与根这一知识点.

| A. | b>0 | B. | b≥0 | C. | b<0 | D. | b∈R |
| A. | x-2y+1=0 | B. | x+2y-3=0 | C. | 2x+y-3=0 | D. | 2x-y-1=0 |
| A. | (x18,x20) | B. | (x17,x19) | C. | (x16,x20) | D. | (x17,x20) |
| A. | $\frac{a}{b}$ | B. | a+b | C. | 2ab | D. | ab |