题目内容
20.已知向量$\overrightarrow{a}$=(cosα,sinα),$\overrightarrow{b}$=(cosβ,sinβ),0<β<α<π.(1)若|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2}$,求证:$\overrightarrow{a}$⊥$\overrightarrow{b}$;
(2)设c=(0,1),若$\overrightarrow{a}$+$\overrightarrow{b}$=c,求α,β的值.
分析 (1)由向量的平方即为模的平方,化简整理,结合向量垂直的条件,即可得证;
(2)先求出$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,根据条件即可得到$\left\{\begin{array}{l}cosα=-cosβ\\ sinα=1-sinβ.\end{array}$,两边分别平方并相加便可得到sinβ=$\frac{1}{2}$,进而得到sinα=$\frac{1}{2}$,根据条件0<β<α<π即可得出α,β.
解答 解:(1)证明:由|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2}$,即($\overrightarrow{a}$-$\overrightarrow{b}$)2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=2,
又因为$\overrightarrow{a}$2=$\overrightarrow{b}$2=|$\overrightarrow{a}$|2=|$\overrightarrow{b}$|2=1.
所以2-2$\overrightarrow{a}$•$\overrightarrow{b}$=2,即$\overrightarrow{a}$•$\overrightarrow{b}$=0,
故$\overrightarrow{a}$⊥$\overrightarrow{b}$;
(2)因为$\overrightarrow{a}$+$\overrightarrow{b}$=(cosα+cosβ,sinα+sinβ)=(0,1),
所以$\left\{\begin{array}{l}cosα+cosβ=0\\ sinα+sinβ=1.\end{array}$,
即$\left\{\begin{array}{l}cosα=-cosβ\\ sinα=1-sinβ.\end{array}$,
两边分别平方再相加得1=2-2sinβ,
∴sinβ=$\frac{1}{2}$,sinα=$\frac{1}{2}$,
又∵0<β<α<π,
∴α=$\frac{5π}{6}$,β=$\frac{π}{6}$.
点评 本题考查向量坐标的加法、减法运算,根据向量坐标求向量长度,向量夹角余弦的坐标公式,以及根据三角函数值求角.

| A. | 1 | B. | -1 | C. | f(1)=1 | D. | f(1)=-1 |
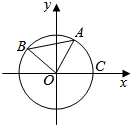 如图A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆与x轴正半轴的交点,△AOB为正三角形,若A点的坐标为(x,y),计∠COA=α.
如图A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆与x轴正半轴的交点,△AOB为正三角形,若A点的坐标为(x,y),计∠COA=α.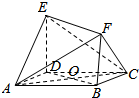 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,连结AC,AC∩BD=0,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,连结AC,AC∩BD=0,