题目内容
已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且椭圆短轴的两个端点与
重合,且椭圆短轴的两个端点与![]() 构成正三角形。
构成正三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与椭圆交于不同两点
与椭圆交于不同两点![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出
恒为定值?若存在,求出![]() 的坐标及定值;若不存在,请说明理由。
的坐标及定值;若不存在,请说明理由。
(Ⅰ) 椭圆的方程为![]()
(Ⅱ) 当![]() 时,
时,![]() 为定值
为定值![]()
解析:
(Ⅰ)由题意知抛物线的焦点![]()
![]() ……………………………………………………………………………1分
……………………………………………………………………………1分
又![]() 椭圆的短轴的两个端点与
椭圆的短轴的两个端点与![]() 构成正三角形
构成正三角形
![]()
![]() 椭圆的方程为
椭圆的方程为![]() ……………………………………………………3分
……………………………………………………3分
(Ⅱ)当直线![]() 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为![]() ,则
,则![]() 的方程为:
的方程为:![]()
![]()
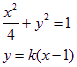
![]()
![]()
![]() ………………………………………5分
………………………………………5分
则![]()
![]()
![]()
![]()
![]()
![]()
![]() ……………………………………7分
……………………………………7分

 ……………………………………9分
……………………………………9分
当![]() 即
即![]() 时
时![]() 为定值
为定值![]() …………………………10分
…………………………10分
当直线![]() 的斜率不存在时,
的斜率不存在时,![]()
由![]() 可得
可得
![]()
![]()
综上所述当![]() 时,
时,![]() 为定值
为定值![]() ………
………

练习册系列答案
相关题目
 的一个焦点与抛物线
的一个焦点与抛物线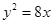 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )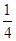 B.
B.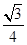 C.
C.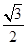 D.
D.
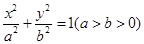 的一个焦点
的一个焦点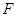 与抛物线
与抛物线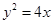 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为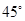 的直线
的直线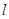 过点
过点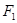 ,问抛物线
,问抛物线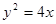 上是否存在一点
上是否存在一点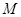 ,使得
,使得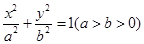 的一个焦点
的一个焦点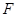 与抛物线
与抛物线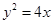 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为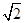 ,倾斜角为
,倾斜角为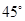 的直线
的直线 过点
过点 ,试求抛物线
,试求抛物线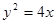 上一点
上一点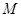 ,使得
,使得 的一个焦点与抛物线
的一个焦点与抛物线 的焦点
的焦点 重合,且椭圆短轴的两个端点与
重合,且椭圆短轴的两个端点与 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点 ,试问在
,试问在 轴上是否存在定点
轴上是否存在定点 ,使
,使 恒为定值? 若存在,求出
恒为定值? 若存在,求出 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由. B.
B. C.
C.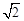 D.2
D.2