题目内容
已知椭圆的一个焦点与短轴的两个端点的连线互相垂直,则此椭圆的离心率为
( )
A. B.
B. C.
C.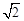 D.2
D.2
【答案】
B
【解析】略

练习册系列答案
相关题目
题目内容
已知椭圆的一个焦点与短轴的两个端点的连线互相垂直,则此椭圆的离心率为
( )
A. B.
B. C.
C.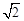 D.2
D.2
B
【解析】略
