题目内容
(本小题满分14分)已知椭圆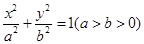 的一个焦点
的一个焦点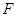 与抛物线
与抛物线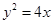 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为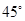 的直线
的直线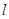 过点
过点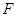 .
.
(1)求椭圆的方程;
(2)设椭圆的另一个焦点为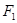 ,问抛物线
,问抛物线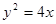 上是否存在一点
上是否存在一点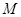 ,使得
,使得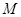 与
与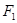 关于直线
关于直线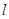 对称,若存在,求出点
对称,若存在,求出点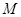 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(1)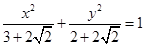 ;
;
(2)抛物线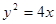 上存在一点
上存在一点 ,使得
,使得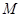 与
与 关于直线
关于直线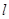 对称.
对称.
【解析】
试题分析:(1)设P(x,y),因为|PF|=2,根据焦半径公式可求出x=1,代入抛物线方程可求点P的坐标.
再根据椭圆的定义: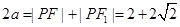 ,求出a,已知c=1,从而可求出
,求出a,已知c=1,从而可求出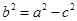 ,故可得椭圆的方程.
,故可得椭圆的方程.
(2)先求出直线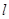 的方程为
的方程为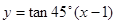 ,即
,即 ,再求出椭圆的另一个焦点为
,再求出椭圆的另一个焦点为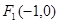 ,可根据点关于直线对称点的求法求出点F1关于直线l的对称点M的坐标,然后代入抛物线方程判定点M是否在抛物线上,从而得到结论.
,可根据点关于直线对称点的求法求出点F1关于直线l的对称点M的坐标,然后代入抛物线方程判定点M是否在抛物线上,从而得到结论.
(1)抛物线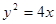 的焦点为
的焦点为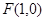 ,………………………1分
,………………………1分
设P(x,y)则|PF|= ,故x=1,y=
,故x=1,y= …………………3分
…………………3分
∴
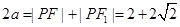 ,
,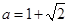 …………………5分
…………………5分
∴  …………………6分
…………………6分
∴
该椭圆的方程为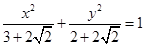 …………………7分
…………………7分
(2)∵ 倾斜角为 的直线
的直线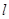 过点
过点 ,
,
∴ 直线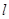 的方程为
的方程为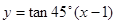 ,即
,即 ,…………………8分
,…………………8分
由(1)知椭圆的另一个焦点为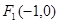 ,设
,设 与
与 关于直线
关于直线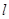 对称,………9分
对称,………9分
则得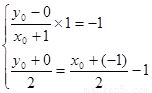 …………………10分
…………………10分
解得 ,即
,即 …………………11分
…………………11分
又 满足
满足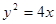 ,故点
,故点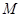 在抛物线上. …………………13分
在抛物线上. …………………13分
所以抛物线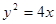 上存在一点
上存在一点 ,使得
,使得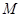 与
与 关于直线
关于直线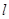 对称.……………14分
对称.……………14分
考点:抛物线及椭圆的定义及标准方程,直线的方程,以及点关于直线的对称.
点评:圆锥曲线的定义是重要的解题工具要引起足够重视,利用它解题很多时候起到化繁为简,另辟捷径的作用.解本小题的第二问要掌握点关于直线的对称点的求法.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)