题目内容
已知△ABC的三边长分别为AB=8,BC=7,AC=3,以点A为圆心,r=2为半径作一个圆,设PQ为⊙A的任意一条直径,记T=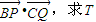 的最大值和最小值,并证明当T取最大值和最小值时,PQ的位置特征是什么.
的最大值和最小值,并证明当T取最大值和最小值时,PQ的位置特征是什么.
【答案】分析:本题考查的知识点是平面向量的数量积运算,由AB=8,BC=7,AC=3,以点A为圆心,r=2为半径作一个圆,设PQ为圆A的任意一条直径,我们易得T=8+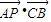 ,又由
,又由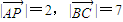 ,我们可得当
,我们可得当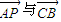 同向时,T取最大值.当
同向时,T取最大值.当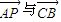 反向时,T取最小值.
反向时,T取最小值.
解答:解:T=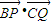
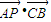
=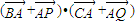
=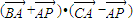
=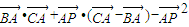
=8+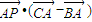
=8+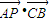
由
故T的最大值为22,T的最小值为-6
此时PQ与BC平行.
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积,有最大值;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数,有最小值.如果两个向量垂直,则它们的夹角为π2,此时向量的数量积,等于0.
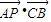 ,又由
,又由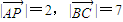 ,我们可得当
,我们可得当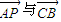 同向时,T取最大值.当
同向时,T取最大值.当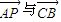 反向时,T取最小值.
反向时,T取最小值.解答:解:T=
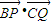
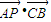
=
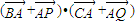
=
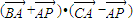
=
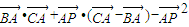
=8+
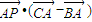
=8+
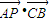
由

故T的最大值为22,T的最小值为-6
此时PQ与BC平行.
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积,有最大值;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数,有最小值.如果两个向量垂直,则它们的夹角为π2,此时向量的数量积,等于0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的三边长为a、b、c,满足直线ax+by+c=0与圆x2+y2=1相离,则△ABC是( )
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |