题目内容
(本小题满分12分)抛物线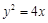 的焦点为F,
的焦点为F,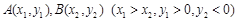 在抛物线上,且存在实数
在抛物线上,且存在实数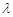 ,使
,使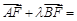
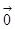 ,
,
(Ⅰ)求直线AB的方程;
(Ⅱ)求△AOB的外接圆的方程。
(Ⅰ)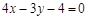 ;(2)
;(2)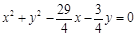 .
.
解析试题分析:(1)先求出抛物线的准线方程,根据 向量关系式
可得到A,B,F三点共线,再由抛物线的定义可表示出| AB|,再设直线AB方程后与抛物线方程进行联立消去y得到关于x的方程,进而可得到两根之和与两根之积,代入到| AB|的表达式中可求出最后k的值,进而得到直线AB的方程.
(2)由(1)中求得的直线方程与抛物线联立可求出A,B的坐标,然后设圆的一般式方程,用待定系数法求出D,E,F的值,得到答案.
解:(Ⅰ)抛物线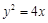 的准线方程为
的准线方程为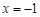 .
.
∵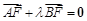 ,∴A,B,F三点共线.由抛物线的定义,得|
,∴A,B,F三点共线.由抛物线的定义,得|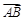 |=
|=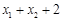 …1分
…1分
设直线AB: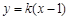 ,而
,而
由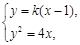 得
得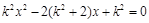 .
.
∴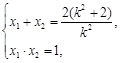 |
|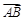 |=
|=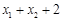 =
= 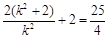 .∴
.∴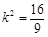 .
.
从而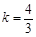 ,故直线AB的方程为
,故直线AB的方程为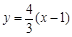 ,即
,即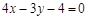
(2)由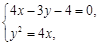 求得A(4,4),B(
求得A(4,4),B( ,-1)
,-1)
设△AOB的外接圆方程为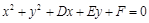 ,则
,则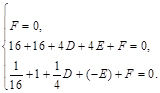 解得
解得
故△AOB的外接圆的方程为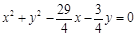 .
.
考点:本试题主要考查了直线与抛物线的综合问题.考查综合运用能力.
点评:解决该试题的关键是能根据向量的工具性得到D,F,E三点共线,然后结合根与系数的关系得到参数的值。

练习册系列答案
相关题目
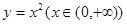 的切线,切点为
的切线,切点为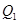 ,设点
,设点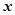 轴上的投影是点
轴上的投影是点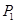 ;又过点
;又过点 的切线,切点为
的切线,切点为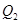 ,设
,设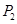 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点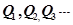
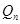 ,设点
,设点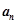 .
.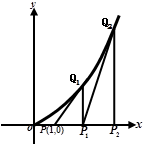
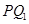 的方程;
的方程;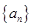 的通项公式;
的通项公式;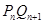 的距离为
的距离为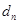 ,求证:
,求证: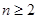 时,
时,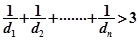
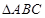 的顶点
的顶点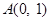 ,
,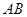 边上的中线
边上的中线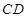 所在的直线方程为
所在的直线方程为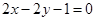 ,
,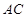 边上的高
边上的高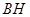 所在直线的方程为
所在直线的方程为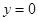 。
。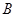 、
、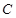 的坐标;
的坐标;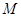 经过不同的三点
经过不同的三点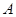 、
、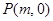 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 ,求圆
,求圆 ,使
,使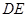 ,以
,以 的图象与
的图象与 轴分别相交于点
轴分别相交于点 两点,向量
两点,向量
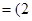 ,
,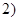 ,又函数
,又函数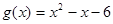 ,且
,且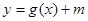 的值域是
的值域是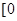 ,
,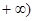 。
。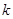 ,
, 及
及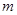 的值;(2)当
的值;(2)当 满足
满足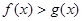 时,求函数
时,求函数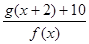 的最小值。
的最小值。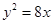 的准线与x轴交于点Q.
的准线与x轴交于点Q. 与抛物线有公共点,求直线
与抛物线有公共点,求直线 :
: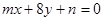 与直线
与直线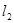 :
: 互相平行,经过点
互相平行,经过点 的直线
的直线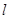 与
与 ,试求直线
,试求直线 且倾斜角为
且倾斜角为 的直线和曲线
的直线和曲线 (
( 为参数)相交于
为参数)相交于 两点.求线段
两点.求线段 的长.
的长.