题目内容
如图,P是抛物线C:y=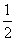 x2上一点,直线l过点P且与抛物线C交于另一点Q,
x2上一点,直线l过点P且与抛物线C交于另一点Q,
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求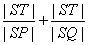 的取值范围。
的取值范围。
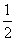 x2上一点,直线l过点P且与抛物线C交于另一点Q,
x2上一点,直线l过点P且与抛物线C交于另一点Q,(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
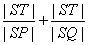 的取值范围。
的取值范围。 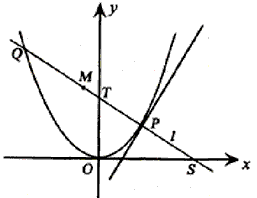
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),
依题意x1≠0,y1>0,y2>0,
由y= x2, ①
x2, ①
得y′=x,
∴过点P的切线的斜率k切=x1,
∴直线l的斜率kl= ,
,
∴直线l的方程为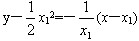 ,
,
联立①②消去y,得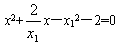 ,
,
∵M是PQ的中点,
∴ ,
,
消去x1,得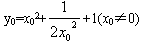 ,
,
∴PQ中点M的轨迹方程为 ;
;
(Ⅱ)设直线l:y=kx+b,
依题意k≠0,b≠0,则T(0,b),
分别过P、Q作PP′⊥x轴,QQ′⊥y轴,垂足分别为P′、Q′,
则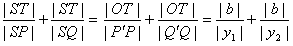 ,
,
由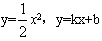 消去x,得y2-2(k2+b)y+b2=0, ③
消去x,得y2-2(k2+b)y+b2=0, ③
则y1+y2=2(k2+b),y1y2=b2,
∴ ,
,
∵y1、y2可取一切不相等的正数,
∴ 的取值范围是(2,+∞)。
的取值范围是(2,+∞)。
依题意x1≠0,y1>0,y2>0,
由y=
 x2, ①
x2, ① 得y′=x,
∴过点P的切线的斜率k切=x1,
∴直线l的斜率kl=
 ,
,∴直线l的方程为
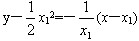 ,
,联立①②消去y,得
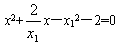 ,
,∵M是PQ的中点,
∴
 ,
,消去x1,得
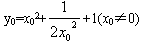 ,
,∴PQ中点M的轨迹方程为
 ;
;(Ⅱ)设直线l:y=kx+b,
依题意k≠0,b≠0,则T(0,b),
分别过P、Q作PP′⊥x轴,QQ′⊥y轴,垂足分别为P′、Q′,
则
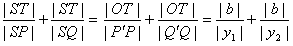 ,
,由
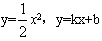 消去x,得y2-2(k2+b)y+b2=0, ③
消去x,得y2-2(k2+b)y+b2=0, ③则y1+y2=2(k2+b),y1y2=b2,
∴
 ,
,∵y1、y2可取一切不相等的正数,
∴
 的取值范围是(2,+∞)。
的取值范围是(2,+∞)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,P是抛物线C:y=
如图,P是抛物线C:y=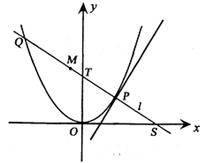 如图,P是抛物线C:y=
如图,P是抛物线C:y= 如图,P是抛物线C:y=
如图,P是抛物线C:y= 如图,P是抛物线C:y=
如图,P是抛物线C:y=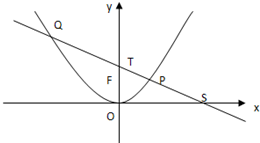 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).