题目内容
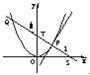 如图,P是抛物线C:y=
如图,P是抛物线C:y=| 1 | 2 |
分析:欲求PQ中点M的轨迹方程,需知P、Q的坐标.思路一,P、Q是直线l与抛物线C的交点,故需求直线l的方程,再与抛物线C的方程联立,利用韦达定理、中点坐标公式可求得M的轨迹方程;思路二,设出P、Q的坐标,利用P、Q的坐标满足抛物线C的方程,代入抛物线C的方程相减得PQ的斜率,利用PQ的斜率就是l的斜率,可求得M的轨迹方程.
解答:解:设P(x1,y1)、Q(x2,y2)、M(x0,y0),依题意知x1≠0,y1>0,y2>0.
由y=
x2,①
得y′=x.
∴过点P的切线的斜率k切=x1,∴直线l的斜率kl=-
=-
,
直线l的方程为y-
x12=-
(x-x1).②
方法一:联立①②消去y,得x2+
x-x12-2=0.
∵M为PQ的中点,
∴x0=
=-
,y0=
x12-
(x0-x1).消去x1,得y0=x02+
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+
+1(x≠0).
方法二:由y1=
x12,y2=
x22,x0=
,
得y1-y2=
x12-
x22=
(x1+x2)(x1-x2)=x0(x1-x2),则x0=
=kl=-
,
∴x1=-
.
将上式代入②并整理,得y0=x02+
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+
+1(x≠0).
由y=
| 1 |
| 2 |
得y′=x.
∴过点P的切线的斜率k切=x1,∴直线l的斜率kl=-
| 1 |
| k切 |
| 1 |
| x1 |
直线l的方程为y-
| 1 |
| 2 |
| 1 |
| x1 |
方法一:联立①②消去y,得x2+
| 2 |
| x1 |
∵M为PQ的中点,
∴x0=
| x1+x2 |
| 2 |
| 1 |
| x1 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| 2x02 |
∴PQ中点M的轨迹方程为y=x2+
| 1 |
| 2x2 |
方法二:由y1=
| 1 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
得y1-y2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| y1-y2 |
| x1-x2 |
| 1 |
| x1 |
∴x1=-
| 1 |
| x0 |
将上式代入②并整理,得y0=x02+
| 1 |
| 2x02 |
∴PQ中点M的轨迹方程为y=x2+
| 1 |
| 2x2 |
点评:本题考查抛物线的应用,及轨迹方程的求法,关键是看清题中给出的条件,灵活运用韦达定理,中点坐标公式进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
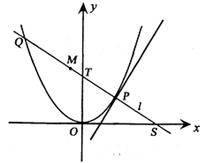 如图,P是抛物线C:y=
如图,P是抛物线C:y=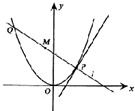 如图,P是抛物线C:y=
如图,P是抛物线C:y=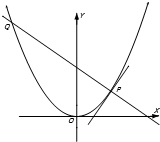 如图,P是抛物线C:y=
如图,P是抛物线C:y= 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).